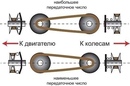
8.4: Передаточное отношение
Передачи используются не только для передачи мощности, но также для обеспечения возможности настройки механического преимущества для механизма. Как обсуждалось во введении к данному блоку, в некоторых случаях электромотор сам по себе обладает достаточной мощностью для выполнения конкретной задачи, но выходные характеристики электромотора не соответствуют требованиям. Электромотор, который вращается ОЧЕНЬ быстро, но при очень малом крутящем моменте , не подходит для подъема тяжелого груза. В таких случаях возникает необходимость использования передаточного отношения для изменения выходных характеристик и создания баланса крутящего момента и скорости.
Представьте себе велосипед: велосипедист обладает ограниченной мощностью, и хочет обеспечить максимальное использование этой мощности в любой момент времени.
Путем изменения механического преимущества изменяется скорость движения. Мощность представляет собой количество проделанной работы в единицу времени. Чем больше количество работы. тем ниже скорость ее выполнения.
Пример 8.1
В примере 8.1 показано, что если на стороне входа рычаг сместится на 1 метр, на стороне выхода рычаг сместится на 4 метра. Разница пропорциональна соотношению между длинами рычагов.
Длина на выходе / Длина на входе = 8 / 2 = 4
Интересно то, что оба расстояния преодолеваются за одно и то же время. Давайте представим, что смещение рычага на входе на 1 метр происходит за 1 секунду, так что скорость движения на входе составляет 1 метр в секунду. В то же время, на выходе смещение на 4 метра также происходит за 1 секунду, так что скорость движения здесь составляет 8 метров в секунду. Скорость на выходе БОЛЬШЕ скорости на входе за счет соотношения между длинами рычагов.
Пример 8.2
В примере 8.2 представлена та же система, что и в примере 8.1, но теперь на вход действует сила, равная 4 ньютонам. Какова равнодействующая сила на выходе?
Прежде всего, необходимо рассчитать приложенный момент в центре вращения, вызванный входной силой, с помощью формул из Блока 7:
Крутящий момент = Сила х Расстояние от центра гравитации = 4 Н х 2 м = 8 Н-м
Далее, необходимо рассчитать равнодействующую силу на выходе:
Сила = Крутящий момент / Расстояние = 8 Н-м / 8 м = 1 ньютон
Глядя на эти два примера, мы видим, что если система смещается на 1 метр под действием входной силы, равной 4 ньютона, то на выходе она сместится на 4 метра под действием силы, равной 1 ньютон.
Мы можем видеть, как механическое преимущество (выраженное в форме рычагов) может быть использовано для управления входной силой в целях получения требуемого выхода. Передачи работают по тому же принципу.
Цилиндрическая прямозубая шестерня по сути представляет собой серию рычагов. Чем больше диаметр шестерни, тем длиннее рычаг.
Пример 8.3
Как видно из примера 8.3, результатом крутящего момента, приложенного к первой шестерне, является линейная сила, возникающая на кончиках ее зубьев. Эта же сила воздействует на кончики зубьев шестерни, с которой зацепляется первая шестерня, заставляя вторую вращаться по действием крутящего момента. Диаметры шестерен становятся длиной рычагов, при этом изменение крутящего момента равносильно соотношению диаметров. Если малые шестерни приводят в движение больше шестерни, крутящий момент увеличивается. Если большие шестерни приводят в движение малые шестерни, крутящий момент уменьшается.
Пример 8.4
В примере 8.4, если входная 36-зубая шестерня поворачивается на расстояние одного зуба (d = ширина 1 зуба), это означает, что она поворачивается на 1/36-ю своего полного оборота (а1 = 360 / 36 = 10 градусов). Поворачиваясь, она приводит в движение 60-зубую шестерню, заставляя последнюю смещаться также на 1 зуб. Тем не менее, для 60-зубой шестерни это означает смещение всего лишь на 1/60-ю полного оборота (а2 = 360 / 60 = 6 градусов).
Когда малая шестерня проходит определенное расстояние в заданный интервал времени, большая шестерня при этом проходить меньшее расстояние. Это означает, что большая шестерня вращается медленнее малой. Этот принцип работает в обоих направлениях. Если малые шестерни приводят в движение больше шестерни, скорость понижается. Если большие шестерни приводят в движение малые шестерни, скорость повышается.
Из примеров 8.1 — 8.4 видно, что отношение между размерами двух зацепляющихся между собой шестерен пропорционально изменению крутящего момента и скорости между ними.
Как обсуждалось выше, количество зубьев шестерни прямо пропорционально ее диаметру, поэтому для расчета передаточного отношения вместо диаметра можно просто считать зубья.
Передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), поэтому представленная выше пара шестерен может быть описана как 12:60 (или 36 к 60).
Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)
Поэтому передаточное число = зубья ведомой шестерни / зубья ведущей шестерни = 60/36 = 1,67
Как обсуждалось выше, передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), так что пара шестерен, представленная выше, может быть выражена как 12:60 (или 12 к 60).
Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)
Поэтому передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 60/12 = 5
Глядя на пример, представленный выше…
Предельный перегрузочный момент второго вала может быть рассчитан по формуле:
Выходной момент = Входной момент х Передаточное число
Выходной момент = 1,5 Н-м х 5 = 7,5 Н-м
Свободная скорость второго вала может быть рассчитана по формуле:
Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 5 = 20 об/мин
Второй вал, таким образом, вращается со свободной скоростью 20 об/мин, при этом предельный перегрузочный момент равен 7,5 Н-м. При понижении скорости крутящий момент увеличивается.
Для второго примера расчеты могут быть произведены тем же способом.
Передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 12/60 = 0,2
Выходной момент = Входной момент х Передаточное число = 1,5 Н-м х 0,2 = 0,3 Н-м
Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 0,2 = 500 об/мин
Второй вал, таким образом, вращается со свободной скоростью 500 об/мин, при этом предельный перегрузочный момент равен 0,3 Н-м. При повышении скорости крутящий момент уменьшается.
При повышении скорости крутящий момент уменьшается.
Передаточное число редуктора
Передаточное отношение: общее определение
Передаточное отношение — это соотношение угловых скоростей или крутящих моментов валов (в зависимости от строения механизма).Передачи применяются для того, чтобы передать вращающий момент от электродвигателя к исполнительному устройству. Почему это необходимо? Дело в том, что сам мотор обычно не может передать требуемый вращающий момент, кроме того, частота вращения вала электродвигателя оказывается слишком велика, поэтому её надо понизить. Для этого и сконструированы понижающие передачи, редукторы. Таким образом удаётся изменить сразу и частоту вращения вала, и крутящий момент.
Существует два способа передачи вращающего момента: жёсткий (момент передается жесткими звеньями, например, шестернями) и фрикционный (момент передается силами трения, работающих на поверхностях вала, например, ременная передача). Также есть возможность совмещать эти способы передачи.
Характеристика зубчатой передачи редуктора
Зубчатая передача редуктора
Зубчатые редукторы очень часто задействуют в машиностроении. Именно их выбирают благодаря большому количеству преимуществ: высокому КПД, долгому сроку службы механизма, маленьким габаритам, постоянству передаточного отношения, простой и надёжной конструкции.
Также у этих редукторов есть и недостатки. К ним относят шум при больших скоростях и большие размеры редукторов, если передаточные отношения велики. Тем не менее, плюсов их использования гораздо больше, чем минусов, что и определяет итоговую востребованность.
 А конечным потребителям в цепочке передачи движения обычно требуется куда меньшая частота. Стоит рассмотреть для лучшего понимания на конкретном примере. Возьмём, скажем, ленту транспортёра. Она движется медленно. Как же сделать так, чтобы надежно передать вращающий момент от электродвигателя к конечному устройству?
А конечным потребителям в цепочке передачи движения обычно требуется куда меньшая частота. Стоит рассмотреть для лучшего понимания на конкретном примере. Возьмём, скажем, ленту транспортёра. Она движется медленно. Как же сделать так, чтобы надежно передать вращающий момент от электродвигателя к конечному устройству? Здесь на помощь как раз и придут многоступенчатые редукторы. Наличие нескольких ступеней позволяет сделать компактное устройство, значительно снижающее частоту вращения вала.
В общем случае общее передаточное отношение редуктора равно отношению частоты вращения входного (ведущего) вала и частоты вращения ведомого (выходного) вала. Отсюда следует, что если выходной вал вращается медленнее входного, то передаточное отношение будет больше единицы. Такие передачи называют понижающими. Если же скорость выходного вала будет выше скорости входного вала, то передаточное число будет меньше единицы. В этом случае говорят о повышающей передаче или мультипликаторе.
При передаче движения всегда соответственно меняется и крутящий момент: если передача понижающая, то момент увеличивается, если повышающая, то уменьшается. Поэтому передаточное число можно представить как отношение крутящего момента на выходе к крутящему моменту на входе в редуктор.
Расчёт без учета сопротивления Любой редуктор состоит из зубчатых пар. Чтобы рассчитать передаточное число каждой пары, надо разделить количество зубьев ведущего колеса на количество зубьев ведомого колеса.
Если в передаче участвует так называемая паразитка, то она в расчете передаточного отношения не участвует, так как ее задача лишь менять направление движения.
Важно! При этом надо смотреть, меняется ли направление вращения шестеренки. Если меняется, то передаточное отношение принимается со знаком минус, если не меняется, то плюс.Направление вращения не меняется, если у колеса нарезка зубьев сделана внутри колеса.
Также при расчете передаточных отношений можно использовать наружный диаметр шестерни. Иногда это удобно, если посчитать число зубьев затруднительно. Важно: зубчатая передача жесткая, здесь нет проскальзывания, как в ременной передаче, поэтому передаточное число всегда можно рассчитать с абсолютной точностью.
Если в редукторе применен червячный редуктор, то его передаточное отношение определяется как отношение числа зубьев ведущего колеса к числу заходов (витков) червяка. Чаще всего у червяка один заход, поэтому ясно: передаточное отношение червячной пары огромно, а вращающий момент может повышаться в десятки раз.
КПД зубчатой передачи Преимуществами данной передачи считаются:
- Большая и неограниченная мощность.
- Небольшая масса и габариты.
- Большой коэффициент полезного действия (приблизительно 0,95-0,99).
- Надёжны, но нуждаются в большой точности изготовления.
КПД определяется как отношение реально полученной энергии к потребленной. Чем выше КПД механизма, тем больше энергии преобразовывается на полезные цели, тем меньше потери, тем эффективнее механизм.
Учёные всего мира постоянно ведут борьбу именно за сокращение непроизводительных потерь. Чтобы обеспечить хорошую работу машины с большим КПД, можно использовать масла с различными свойствами при больших изменениях температуры среды. При экспериментах с различными видами масла совместно с допустимой нагрузочной способности зубчатых передач на рабочих поверхностях зубьев не обнаружили развитие процесса разрушения, что обеспечивает отличные технико-экономические показатели машины.
Важно! КПД зубчатой передачи сильно зависит от точности изготовления зубчатых колес.
 В случае грубых нарушений геометрии в редукторе будут большие расходы энергии, он будет нагреваться, его КПД значительно упадёт. Поэтому редукторы следует приобретать только у проверенных производителей.
В случае грубых нарушений геометрии в редукторе будут большие расходы энергии, он будет нагреваться, его КПД значительно упадёт. Поэтому редукторы следует приобретать только у проверенных производителей. Постоянное и переменное передаточное отношение редуктора Передаточное отношение может быть как постоянным, так и переменным. При переменном случае оно может меняться бесступенчато или ступенчато. В промышленности нашли применение обе эти схемы. Если передаточное число меняется плавно, то такое устройство называют вариатором. Эти устройства дороги и требуют точной сборки и квалифицированного обслуживания. Но всё это оправдывается конечным результатом — их полезность уже проверена временем.
Передаточное число это отношение
Рассматривая тему деталей машин, нельзя не уделить внимания такому важному техническому показателю, как передаточное отношение. Этот термин существует уже достаточно давно и о его значении в механике стоит поговорить отдельно.
Формулировка
Передаточное отношение – одна из самых важных технических характеристик любой механической передачи вращательного движения. С практической точки зрения, описываемый показатель позволяет понять, во сколько раз вырастает момент силы в результате функционирования передачи. Определение передаточных отношений в любом механизме – одна из самых главных задач в механике и машиностроении.
Некоторые тонкости
Передаточное отношение определяется при наличии как минимум двух зубчатых колес (шестерен), которые находятся в зацеплении между собой. Такое сопряжение именуется зубчатой передачей.
Самый простой способ рассчитать передаточное число – посчитать количество зубьев на каждом из имеющихся колес, а после произвести деление числа зубьев ведомой шестерни на количество колес ведущей шестерни. Данное рациональное число и будет являться передаточным отношением.
Важно иметь в виду, что в случае определения передаточного числа в зубчатой передаче, имеющей несколько шестерен, необходимо опять-таки делить количество зубьев ведущего колеса на количество ведомого. При этом параметры промежуточных шестерен не учитываются.
При этом параметры промежуточных шестерен не учитываются.
Обзор передач
На сегодняшний день существуют такие виды механических передач:
В целом же, механические передачи разделяются по таким критериям:
- В зависимости от передачи движения от ведущего звена к ведомому: передачи трением и передачи зацеплением.
- В зависимости от соотношения скоростей ведомого и ведущего звеньев: замедляющие передачи (они же редукторы), ускоряющие передачи (мультипликаторы).
- В зависимости от расположения осей валов: передачи с перекрещивающимися, пересекающимися и параллельными осями.
Стоит указать, что замедляющие передачи на практике применяются гораздо чаще, нежели ускоряющие. Этот факт объясняется тем, что скорости вращения двигателей зачастую гораздо выше требуемой скорости вала исполнительного механизма или машины.
Зубчатая передача
Передаточное отношение зубчатой передачи можно вычислять не только по соотношению зубьев ее колес, но также путем деления значения угловой скорости ведомого вала на угловую скорость ведущего вала, а также благодаря соотношению числа оборотов ведомого и ведущего валов.
Диапазон передаточного отношения может быть очень велик и достигать больших значений. При этом само по себе передаточное отношение зубчатой передачи характеризуется постоянством, так как зацепление не подвержено проскальзыванию. Коэффициент полезного действия такой передачи находится в пределах 0,97-0,98.
Зубчатые передачи передают вращение между валами, которые могут иметь параллельные, скрещивающиеся или перпендикулярные оси. Кроме того, такие передачи способны трансформировать (преобразовывать) поступательное движение во вращательное и наоборот (передчи «винт-гайка»).
Зацепление в зубчатых передачах может быть как внешним, так и внутренним. Колеса изготавливаются с прямыми, косыми или шевронными зубьями.
Зубчатые передачи способны передавать большие скорости вращения с постоянным передаточным отношением и имеют высокий КПД.
Передаточное отношение редуктора является одним из важнейших критериев в процессе его выбора. Вторым по важности показателем считается межосевое расстояние.
Червячная передача
Используется для передачи вращательного движения в тех случаях, когда оси валов перекрещиваются.
Червяк может быть цилиндрическим или глобоидным в зависимости от поверхности расположения резьбы, а также может быть эвольвентным или архимедовым (в данном случае решающую роль играет профиль резьбы).
Основными недостатками описываемой передачи можно считать:
- Высокий показатель тепловыделения.
- Частое заедание и невысокий КПД.
Волновая передача
Ее работа основывается на принципе трансформации параметров движения благодаря волновому деформированию гибкого элемента механизма. По сути, такая передача является разновидностью планетарной передачи.
В состав волновой передачи входит жесткое колесо зубчатое, имеющее внутренние зубья, и вращающееся гибкое колесо с наружными зубьями. Оба колеса между собой входят в зацепление благодаря генератору волн, соединенному непосредственно с корпусом передачи.
За счет имеющихся конструктивных особенностей волновая передача наделена следующими достоинствами:
- Небольшие габариты и масса.
- Высокая кинематическая точность.
- Передаточное отношение передачи в одной ступени имеет большой показатель и вполне может достигать 300.
- Идеальная демпфирующая способность.
- Формирование в одной ступени большого передаточного отношения.
К недостаткам же относятся:
- Весьма сложная конструкция.
- Высокие потери мощности на трение и деформацию гибкого колеса (КПД составляет порядка 0,7-0,85).
Фрикционная передача
Чаще всего применяется в текстильной отрасли, станкостроении и прочих сферах промышленности, кроме авиастроения. Передаваемая мощность может достигать 10 кВт. При больших показателях очень трудно гарантировать требуемое усилие прижатия катков.
В передаче существует три вида скольжения: геометрическое, упругое и буксование.
Для нормально функционирующей передачи характерно именно упругое скольжение, в то время как буксование говорит о наличии перегрузки.
Ременная передача
Как и зубчатая она встречается очень часто. В зависимости от того, как располагаются валы и ремень, передача может быть:
- Открытой.
- Перекрестной.
- Полуперекрестной.
- Угловой.
- Спаренной.
- Ступенчатой.
Ремень может быть круглым, плоским, трапецеидальным.
Передаточное отношение в таких передачах находится в пределах 1:4, 1:5 и лишь в редких случаях может быть равно 1:8.
К положительным качествам ременной передачи следует отнести:
- Простоту конструкции.
- Возможность расположения обоих шкивов на большом расстоянии друг от друга (свыше 15 метров).
- Бесшумность и плавность работы.
- Защиту механизмов от перегрузок благодаря упругим свойствам ремня и его способности в определённые моменты проскальзывать по поверхностям шкивов.
- Работу при больших угловых скоростях.
Недостатками передачи являются:
- Удлинение ремней (их вытягивание) в процессе работы, то есть недолговечность.
- Непостоянство передаточного числа, что объясняется неизбежным проскальзыванием ремня.
- Достаточно большие размеры.
Цепная передача
В отличие от ременного аналога не подвержена проскальзыванию. Расчет передаточного отношения выполняется по аналогии с зубчатой передачей, ведь звездочки передачи, по сути, представляют собой те же зубчатые колеса.
Характерная особенность цепной передачи – вращение передается исключительно при наличии параллельных валов. Между осями звёздочек расстояние необходимо принимать не менее величины полутора диаметров большой звездочки. При этом передаточное число может достигать показателя 1:15.
Также важно заметить, что цепь надевается на звездочки не с натягом, как ремни, а с определенной степенью провисания.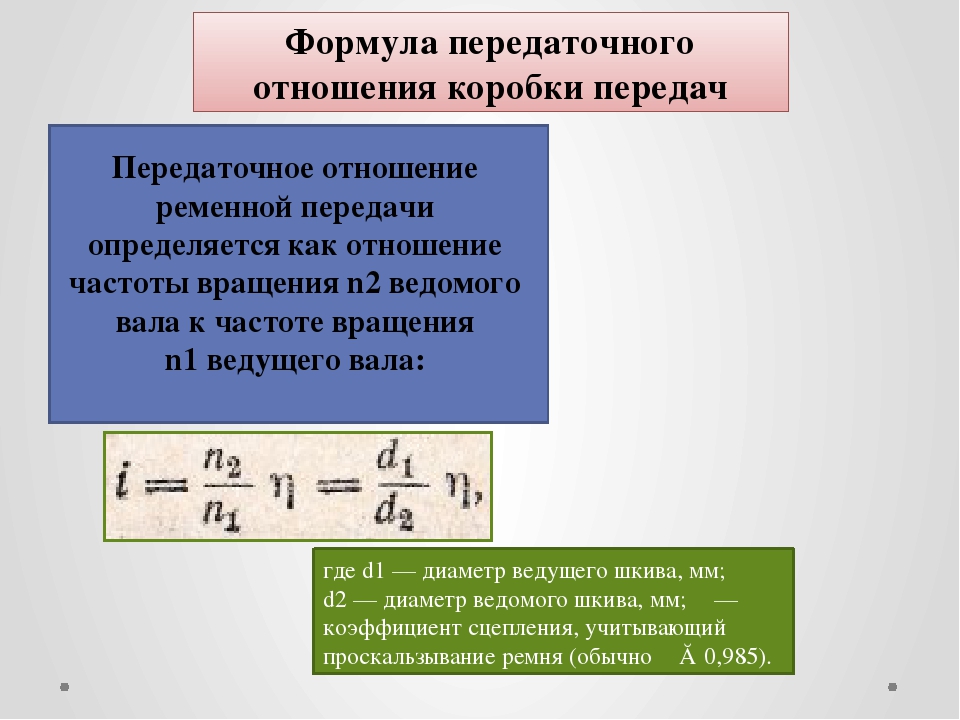 Регулировка натяжения проводится с помощью специального винта.
Регулировка натяжения проводится с помощью специального винта.
Достоинства передачи таковы:
- Небольшая чувствительность к неточностям установки валов.
- Передача вращения может осуществляться одной цепью сразу же нескольким звездочкам.
- Вращение может передаваться на большие расстояния.
Недостатком же является высокий шум и износ цепей в случае некачественного монтажа и при плохом техническом обслуживании.
Храповый механизм
Во многих машинах и агрегатах применяется не только непрерывное вращательное движение, но и прерывистое тоже, которое осуществляется с помощью храповика, собачки и рычага.
Храповый механизм помимо вращения еще и осуществляет предохранительную функцию. Так, например, в грузоподъемных лебедках, храповик совместно с собачкой не позволяют барабану проворачиваться в обратную сторону, надёжно фиксируя его в требуемом пространственном положении.
Рассмотренные виды механических передач применяются практически в любой отрасли народного хозяйства и получили широчайшее распространение благодаря своим техническим возможностям.
Передачи используются не только для передачи мощности, но также для обеспечения возможности настройки механического преимущества для механизма. Как обсуждалось во введении к данному блоку, в некоторых случаях электромотор сам по себе обладает достаточной мощностью для выполнения конкретной задачи, но выходные характеристики электромотора не соответствуют требованиям. Электромотор, который вращается ОЧЕНЬ быстро, но при очень малом крутящем моменте , не подходит для подъема тяжелого груза. В таких случаях возникает необходимость использования передаточного отношения для изменения выходных характеристик и создания баланса крутящего момента и скорости.
Представьте себе велосипед: велосипедист обладает ограниченной мощностью, и хочет обеспечить максимальное использование этой мощности в любой момент времени.
Путем изменения механического преимущества изменяется скорость движения. Мощность представляет собой количество проделанной работы в единицу времени. Чем больше количество работы. тем ниже скорость ее выполнения.
Мощность представляет собой количество проделанной работы в единицу времени. Чем больше количество работы. тем ниже скорость ее выполнения.
В примере 8.1 показано, что если на стороне входа рычаг сместится на 1 метр, на стороне выхода рычаг сместится на 4 метра. Разница пропорциональна соотношению между длинами рычагов.
Длина на выходе / Длина на входе = 8 / 2 = 4
Интересно то, что оба расстояния преодолеваются за одно и то же время. Давайте представим, что смещение рычага на входе на 1 метр происходит за 1 секунду, так что скорость движения на входе составляет 1 метр в секунду. В то же время, на выходе смещение на 4 метра также происходит за 1 секунду, так что скорость движения здесь составляет 8 метров в секунду. Скорость на выходе БОЛЬШЕ скорости на входе за счет соотношения между длинами рычагов.
В примере 8.2 представлена та же система, что и в примере 8.1, но теперь на вход действует сила, равная 4 ньютонам. Какова равнодействующая сила на выходе?
Прежде всего, необходимо рассчитать приложенный момент в центре вращения, вызванный входной силой, с помощью формул из Блока 7:
Крутящий момент = Сила х Расстояние от центра гравитации = 4 Н х 2 м = 8 Н-м
Далее, необходимо рассчитать равнодействующую силу на выходе:
Сила = Крутящий момент / Расстояние = 8 Н-м / 8 м = 1 ньютон
Глядя на эти два примера, мы видим, что если система смещается на 1 метр под действием входной силы, равной 4 ньютона, то на выходе она сместится на 4 метра под действием силы, равной 1 ньютон. При меньшей силе рычаг смещается быстрее!
Мы можем видеть, как механическое преимущество (выраженное в форме рычагов) может быть использовано для управления входной силой в целях получения требуемого выхода. Передачи работают по тому же принципу.
Цилиндрическая прямозубая шестерня по сути представляет собой серию рычагов. Чем больше диаметр шестерни, тем длиннее рычаг.
Как видно из примера 8.3, результатом крутящего момента, приложенного к первой шестерне, является линейная сила, возникающая на кончиках ее зубьев. Эта же сила воздействует на кончики зубьев шестерни, с которой зацепляется первая шестерня, заставляя вторую вращаться по действием крутящего момента. Диаметры шестерен становятся длиной рычагов, при этом изменение крутящего момента равносильно соотношению диаметров. Если малые шестерни приводят в движение больше шестерни, крутящий момент увеличивается. Если большие шестерни приводят в движение малые шестерни, крутящий момент уменьшается.
Эта же сила воздействует на кончики зубьев шестерни, с которой зацепляется первая шестерня, заставляя вторую вращаться по действием крутящего момента. Диаметры шестерен становятся длиной рычагов, при этом изменение крутящего момента равносильно соотношению диаметров. Если малые шестерни приводят в движение больше шестерни, крутящий момент увеличивается. Если большие шестерни приводят в движение малые шестерни, крутящий момент уменьшается.
В примере 8.4, если входная 36-зубая шестерня поворачивается на расстояние одного зуба (d = ширина 1 зуба), это означает, что она поворачивается на 1/36-ю своего полного оборота (а1 = 360 / 36 = 10 градусов). Поворачиваясь, она приводит в движение 60-зубую шестерню, заставляя последнюю смещаться также на 1 зуб. Тем не менее, для 60-зубой шестерни это означает смещение всего лишь на 1/60-ю полного оборота (а2 = 360 / 60 = 6 градусов).
Когда малая шестерня проходит определенное расстояние в заданный интервал времени, большая шестерня при этом проходить меньшее расстояние. Это означает, что большая шестерня вращается медленнее малой. Этот принцип работает в обоих направлениях. Если малые шестерни приводят в движение больше шестерни, скорость понижается. Если большие шестерни приводят в движение малые шестерни, скорость повышается.
Из примеров 8.1 – 8.4 видно, что отношение между размерами двух зацепляющихся между собой шестерен пропорционально изменению крутящего момента и скорости между ними. Это называется передаточным числом.
Как обсуждалось выше, количество зубьев шестерни прямо пропорционально ее диаметру, поэтому для расчета передаточного отношения вместо диаметра можно просто считать зубья.
Передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), поэтому представленная выше пара шестерен может быть описана как 12:60 (или 36 к 60).
Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)
Поэтому передаточное число = зубья ведомой шестерни / зубья ведущей шестерни = 60/36 = 1,67
Как обсуждалось выше, передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), так что пара шестерен, представленная выше, может быть выражена как 12:60 (или 12 к 60).
Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)
Поэтому передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 60/12 = 5
Глядя на пример, представленный выше.
Предельный перегрузочный момент второго вала может быть рассчитан по формуле:
Выходной момент = Входной момент х Передаточное число
Выходной момент = 1,5 Н-м х 5 = 7,5 Н-м
Свободная скорость второго вала может быть рассчитана по формуле:
Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 5 = 20 об/мин
Второй вал, таким образом, вращается со свободной скоростью 20 об/мин, при этом предельный перегрузочный момент равен 7,5 Н-м. При понижении скорости крутящий момент увеличивается.
Для второго примера расчеты могут быть произведены тем же способом.
Передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 12/60 = 0,2
Выходной момент = Входной момент х Передаточное число = 1,5 Н-м х 0,2 = 0,3 Н-м
Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 0,2 = 500 об/мин
Второй вал, таким образом, вращается со свободной скоростью 500 об/мин, при этом предельный перегрузочный момент равен 0,3 Н-м. При повышении скорости крутящий момент уменьшается.
Передаточное отношение – это отношение мгновенных угловых или линейных скоростей ведущего и ведомого звеньев. u = ω1/ω2.
Зубчатая и червячная передачи. Зубчатая передача является связующим звеном двух или более валов, либо вала с рейкой. Зубчатая передача от ведущего вала к ведомому служит для того, чтобы крутящие моменты и угловые скорости этих валов находились в требуемом отношении по величине и направлению.
Передаточным отношением зубчатой пары называется отношение угловых скоростей сопряженных зубчатых колес. В зависимости от числа ступеней, участвующих в изменении угловой скорости между ведущим и ведомым валами, зубчатые колеса разделяются на одноступенчатые, двухступенчатые, трехступенчатые и т. д.
д.
Ременные передачи.Ременная передача осуществляется при помощи двух шкивов, закрепленных на валах, и надетого на эти шкивы с натяжением бесконечного ремня, имеющего прямоугольное, трапециевидное и реже круглое сечение (плоские, клиновые и круглые ремни. Наибольшее распространение получили плоские ремни — кожаные, хлопчатобумажные, пропитанные резиной, или хлопчатобумажные тканые.
Для создания и поддержания натяжения ремня в плоскоременной передаче применяют натяжной ролик
Цепная передача.Применяемые в станках цепи по характеру выполняемой работы делятся на три основные группы: приводные, грузовые и тяговые. Приводные цепи в большинстве случаев осуществляют передачу от источника движения или какого-либо передаточного механизма к приемному узлу станка. Цепи могут работать с большими скоростями (до 30 м/сек), как при малых, так и при больших межцентровых расстояниях. Приводные цепи имеют ту особенность, что одной цепью можно соединить и приводить в движение одновременно несколько валов.
Фрикционная передача.Фрикционные передачи нашли применение в приводах главного движения и приводах подачи универсальных станков.
Планетарные эпициклические передачи.Планетарным зубчатым механизмом называется механизм, имеющий зубчатые колеса с движущимися геометрическими осями. Такие колеса называются планетарными или сателлитами. Система, которая несет оси сателлитов, называется водилом. Колеса с неподвижными осями, по которым обкатываются сателлиты, называются центральными. Неподвижные центральные колеса называются опорными. Эпициклические механизмы применяются для получения больших передаточных отношений и для цепей суммирования двух независимых движений в механизмах затыловочных, расточных, зуборезных, автоматических станков и в делительных головках фрезерных станков.
17. Точение. Геометрия токарного резца. Классификация токарных резцов. Операции, выполняемые на токарных станках.
Токарная обработка (точение) — это механическая обработка резанием наружных и внутренних поверхностей вращения, в том числе цилиндрических и конических, торцевание, отрезание, снятие фасок, обработка галтелей, прорезание канавок, нарезание внутренних и наружных резьб на токарных станках.
Классификация токарных резцов
Для токарной обработки применяют разнообразные резцы. В зависимости от направления движения подачи различают левые и правые резцы.
По форме и расположению головки относительно стержня резцы могут быть прямые, отогнутые и оттянутые.
По назначению различают проходные, упорные, подрезные (торцовые), прорезные, отрезные, фасонные, резьбовые и расточные резцы.
Инструментальные материалы делят на следующие три группы.
Первая группа — материалы дня инструментов, работающих на низких скоростях резания. К ним относятся высококачественные углеродистые инструментал ь-ные стали (У10А, У11А, У12А)
Вторая группа — материалы для инструментов, работающих на повышенных скоростях резания, — быстрорежущие стали Р9, Р12.
Третья группа — материалы для инструментов, работающих на высоких скоростях резания,-металлокерамические твердые сплавы, выпускаемые в виде пластинок различных размеров и форм.
Классификация резцов по способу крепления режущей части. а-цельный, б-сварной, в-с наплавленной пластинкой, г-с механическим креплением пластинки.
Основные операции на токарных станках.
Обтачивание гладких цилиндрических поверхностей. Гладкие цилиндрические поверхности деталей обтачивают проходными резцами в два приема. Сначала черновым резцом производят обдирку — грубое обтачивание, — быстро снимая основную массу лишнего металла.
Подрезание торцов и уступов.Для подрезания торцов и уступов на токарном станке пользуются обычно подрезными резцами.
Вытачивание канавокДля вытачивания канавок служат прорезные резцы. Их режущая кромка точно воспроизводит форму канавки. Так как ширина канавок обычно невелика, режущую кромку прорезного резца приходится делать узкой, поэтому она получается довольно ломкой. Для повышения прочности такого резца высоту его головки делают в несколько раз больше ширины.
Вытачивание конусов. В практике юного токаря вытачивание конусов будет встречаться реже, чем другие работы. Наиболее простой способ— точение небольших конусов (не более 20 мм) специальным широким резцом.
В практике юного токаря вытачивание конусов будет встречаться реже, чем другие работы. Наиболее простой способ— точение небольших конусов (не более 20 мм) специальным широким резцом.
Обработка внутренних поверхностей.Обработка отверстий может производиться различными инструментами, в зависимости от требуемой формы поверхности и точности обработки.
Сверление и рассверливание. Неглубокие отверстия на токарном станке сверлят перовыми и спиральными (цилиндрическими) сверлами. Перовое сверло имеет плоскую лопатку с двумя режущими кромками, переходящую в стержень. Точность отверстия при обработке перовым сверлом невелика, поэтому его употребляют тогда, когда большой точности не требуется.
Передаточное число (отношение) редуктора
Прежде всего, необходимо разобраться, что такое передаточное число редуктора. Рассмотрим на примере червячного одноступенчатого универсального редуктора Ч-100-40. В данном случае цифра 40 обозначает передаточное число (отношение) редуктора. Что это значит: при вращении быстроходного вала (входного) тихоходный вал (выходной) должен сделать один оборот вокруг своей оси за 40 оборотов входного вала.
Далее необходимо понимать различие между двумя понятиями: передаточное число фактическое и передаточное число номинальное. Номинальное передаточное число – это округленное фактическое передаточное число, это необходимо для удобства и стандартизации обозначения. Пример: редуктор Ч-100 может иметь передаточное отношение фактическое 7,75, а номинальное будет равно 8 и так далее: 10=10; 12=12,5; 15,5=16; 20=20; 24=25; 31=31,5; 40=40; 48=50; 64=63; 84=80.
Теперь рассмотрим способы определения передаточного числа редуктора, в случае если не читается бирка и отсутствует, какая либо документация на оборудование.
- Первый способ универсален для практически любого типа редуктора или редукторной части оборудования, будь то червячный, цилиндрический, конический, планетарный и так далее редуктор.
 Для этого необходимо покрутить быстроходный вал и количество его оборотов за один оборот тихоходного вала и будет означать фактическое передаточное число.
Для этого необходимо покрутить быстроходный вал и количество его оборотов за один оборот тихоходного вала и будет означать фактическое передаточное число. - Второй способ применяется в случае первого варианта и отсутствием возможности прокрутить и посчитать обороты выходного вала. Здесь существуют различия между методами определения передаточного числа червячного редуктора и, например цилиндрического:
А. Рассмотрим на примере червячного одноступенчатого универсального редуктора 1Ч-160.
Прежде всего, необходимо посчитать количество зубов червячного колеса фото № 1.
У нас получилось 32 зуба.
Затем количество заходов витка на червячном валу фото № 2.
Количество заходов 1.
Теперь 32 делим на 1 получается фактическое передаточное число редуктора 1Ч-160 равное 32.
Теперь рассмотрим способ подсчета передаточного числа червячного редуктора на примере Ч-125.
Считаем количество зубов на червячном колесе фото № 3.
У нас получается 52 зуба.
И считает количество заходов витка на червячном валу фото № 4 и № 5.
У нас получилось число равное 4.
Теперь 52 делим на 4 получается фактическое передаточное число редуктора Ч-125 равное 13.
Б.
Какое передаточное число лучше — Авто журнал КарЛазарт
Чем выше передаточное число редуктора тем
Настройка КПП и редуктора.
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Передаточное число – это основная характеристика отношения передачи крутящего момента от вала двигателя к ведущим колёсам.
Чем больше передаточное число, тем лучше ускорение, но хуже максимальная скорость.
Чем меньше передаточное число, тем хуже ускорение, но максимальная скорость выше.
Передаточные числа механической 6-ти ступенчатой КПП находятся в следующих
диапазонах:
1-я передача – от 4 до 5;
2-я передача – от 2 до 2,6;
3-я передача – от 1,4 до 2;
4-я передача – от 1 до 1,6;
5-я передача – от 0,8 до 1. 4;
4;
6-я передача – от 0.6 до 1; (последнюю передачу, как правило, делают длинной для увеличения максимальной скорости)
задний ход – от 3 до 4.
Передаточное число главной пары редуктора.
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Чем оно выше, тем автомобиль лучше тянет на всех передачах, но максимальная скорость при этом ниже и приходится чаще переключать передачи.
Уменьшая передаточное число, повышают максимальную скорость (если двигатель обладает достаточным запасом мощности), но при этом ухудшается разгон.
Передаточное число главной пары редуктора находится в следующем диапазоне:
3.8 – 4.5
Перейти на новый GT форум
Обьясните пожалуйста, что означают передаточные числа.Много слышал, но конкретно ничего. Пример Mitsubishi Lancer Evo VII
I 2,928
II 1,950
III 1,407
IV 1,031
V 0,720
з.х. 3,416
Главная передача 4,529
Что означают эти цифры? Как узнать склонна ли машина к быстрому разгону или наоборот к достижению максимальной скорости? Возможно ли их изменить? Заранее спасибо.
Вот коротенько :
Передаточное число – это отношение числа зубьев ведомой шестерни к числу зубцов ведущей шестерни. Применительно к ступеням КПП с разными передаточными числами – чем оно больше, тем передача «короче» и «тяговитее», то есть мотор быстрее раскручивается до максимальных оборотов – автомобиль интенсивнее ускоряется из-за быстрой раскрутки, но снижается максимальная скорость на данной передаче. Следовательно, возникает необходимость в частом переключении. На разгонную динамику влияет в такой же степени и передаточное число главной пары редуктора. Чем оно выше, тем автомобиль динамичнее, лучше тянет на всех передачах, но максимальная скорость при этом ниже. При уменьшении передаточного числа получают выигрыш в максимальной скорости (если у двигателя есть запас мощности), но проигрывают в разгонной динамике автомобиля. Например, установка главной пары 4,1 или 4,3 вместо 3,9 превращает стандартную «шестерку» в более динамичный автомобиль.
Правильный подбор передаточных чисел главной пары редуктора, пар шестерен КПП – залог согласованной работы трансмиссии. Эти числа подбираются в зависимости от мощностных и моментных характеристик двигателя, размера колес, возможностей тормозной системы, а в процессе тюнинга автомобиля еще и учитываются пожелания автовладельца
Установка передаточного числа.
При постоянной выходной мощности двигателя ускорение и максимальная скорость, зависит от передаточного числа.
Передаточное число — это сколько оборотов двигателя ведущей шестерни приходится на один оборот шестерни двигателя.
Высокое передаточное число (п.ч.) обеспечивается шестерней с наименьшим количеством зубьев, а малое — шестерней с наибольшим количеством зубьев. С высоким передаточным числом вы получаете хорошие ускорение, но маленькую максимальную скорость. Машина же с низким п.ч. будет обладать хорошей максимальной скоростью, но будет медленно разгоняться. Машина с высоким п.ч. годится для трассы состоящей из сложных кривых, где прохождение трассы осуществляется на малых скоростях, машина же с низким п.ч. будет фаворитом на скоростных трассах. Но слишком низкое п.ч. может перегрузить двигатель и вызвать его перегрев, впоследствии выход его (двигателя) из строя.
Большое п. ч. Маленькое п. ч.
Максимальная скорость Маленькая Высокая
Ускорение Хорошее Не большое
Срок службы
двигателя Продолжительный Короткий
Трасса Техническая Скоростная
Передаточноые числа — это отношение оборотов на входе и на выходе коробки передач (немного утрировано). Т. е. если на первой у Эво 6 отношение 2,928, то обороты выходного вала коробки будут почти в 3 раза меньше, чем обороты лвигателя. то же самое и с главной парой.
Соответственно получаем — максималка выше — если эти отношения меньше (т. е. главная передача , ну, допустим 4, а не 4,529) и наоборот.
Изменить в машине, тем более в Эво можно все, но это как говориться вопрос времени и денег.
Спасибо за ответы.
Архив GT форума
Toyota — Nissan — Mitsubishi — Honda — Mazda — Subaru — Suzuki — Isuzu — Daihatsu
1990 — 1991 — 1992 — 1993 — 1994 — 1995 — 1996 — 1997 — 1998 — 1999 — 2000 — 2001 — 2002 — 2003 — 2004 — 2005 — 2006 — 2007 — 2008 — 2009 — 2010 — 2011 — 2012 — 2013 — 2014 — 2015 — 2016 — 2017 — 2018 — 2019
Прежде всего, необходимо разобраться, что такое передаточное число редуктора. Рассмотрим на примере червячного одноступенчатого универсального редуктора Ч-100-40. В данном случае цифра 40 обозначает передаточное число (отношение) редуктора. Что это значит: при вращении быстроходного вала (входного) тихоходный вал (выходной) должен сделать один оборот вокруг своей оси за 40 оборотов входного вала.
Далее необходимо понимать различие между двумя понятиями: передаточное число фактическое и передаточное число номинальное. Номинальное передаточное число – это округленное фактическое передаточное число, это необходимо для удобства и стандартизации обозначения. Пример: редуктор Ч-100 может иметь передаточное отношение фактическое 7,75, а номинальное будет равно 8 и так далее: 10=10; 12=12,5; 15,5=16; 20=20; 24=25; 31=31,5; 40=40; 48=50; 64=63; 84=80.
Теперь рассмотрим способы определения передаточного числа редуктора, в случае если не читается бирка и отсутствует, какая либо документация на оборудование.
- Первый способ универсален для практически любого типа редуктора или редукторной части оборудования, будь то червячный, цилиндрический, конический, планетарный и так далее редуктор. Для этого необходимо покрутить быстроходный вал и количество его оборотов за один оборот тихоходного вала и будет означать фактическое передаточное число.
- Второй способ применяется в случае первого варианта и отсутствием возможности прокрутить и посчитать обороты выходного вала. Здесь существуют различия между методами определения передаточного числа червячного редуктора и, например цилиндрического:
А.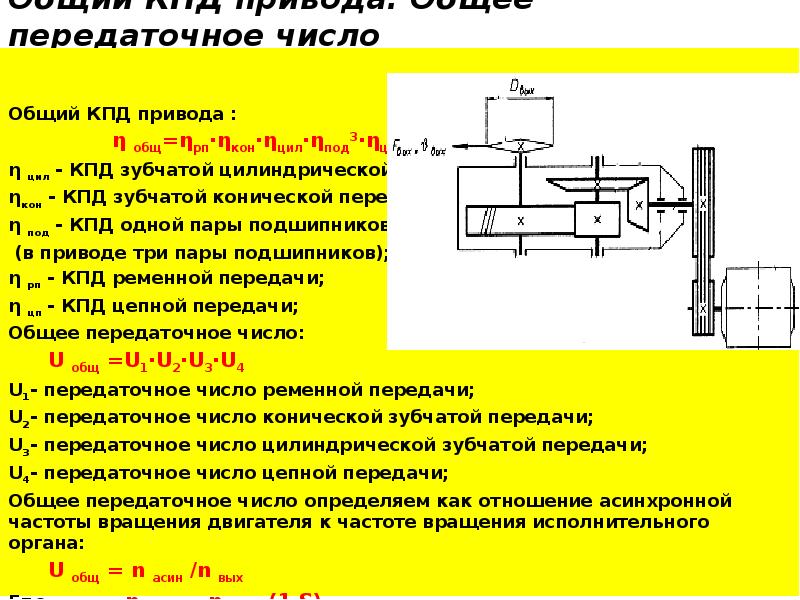 Рассмотрим на примере червячного одноступенчатого универсального редуктора 1Ч-160.
Рассмотрим на примере червячного одноступенчатого универсального редуктора 1Ч-160.
Прежде всего, необходимо посчитать количество зубов червячного колеса фото № 1.
У нас получилось 32 зуба.
Затем количество заходов витка на червячном валу фото № 2.
Количество заходов 1.
Теперь 32 делим на 1 получается фактическое передаточное число редуктора 1Ч-160 равное 32.
Теперь рассмотрим способ подсчета передаточного числа червячного редуктора на примере Ч-125.
Считаем количество зубов на червячном колесе фото № 3.
У нас получается 52 зуба.
И считает количество заходов витка на червячном валу фото № 4 и № 5.
У нас получилось число равное 4.
Теперь 52 делим на 4 получается фактическое передаточное число редуктора Ч-125 равное 13.
0 0 голос
Рейтинг статьи
Передаточное число в редукторе
Передаточное число представляет собой один из важнейших показателей в работе тех или иных механизмов. Данное число означает соотношение количество зубьев шестерне, которая является ведомой, к количеству зубьев ведущего элемента. В качестве такового используется редуктор.
Работа зубчатой передачи обеспечивает работу механизма за счет передачи крутящего момента. То есть именно передаточное число обуславливает работу привода в результате работы двигателя внутреннего сгорания.
Данный показатель имеет существенное значение, поскольку именно он выражает эффективность работы редуктора и коэффициент полезного действия. Это утверждение следует проиллюстрировать несколькими фактами:
• Передаточное число непосредственно влияет на возможность контроля за передаваемым моментом, его величиной. А это позволяет повышать или сокращать передаваемый момент;
• Крутящий момент обуславливает способность автомобиля набирать скорость.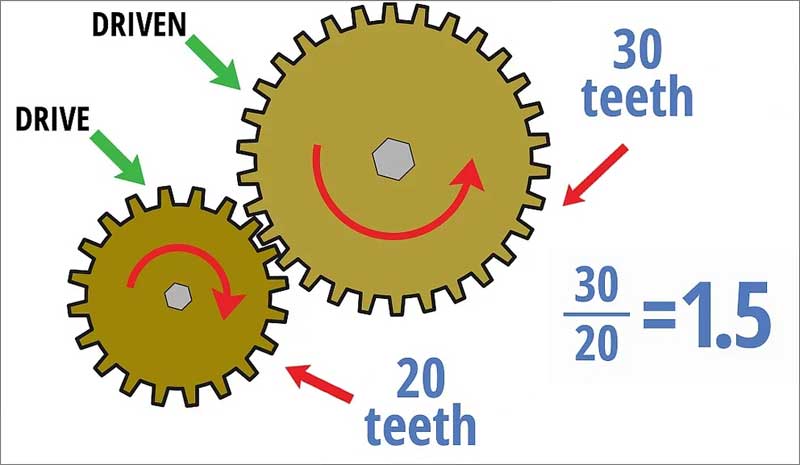 При этом от его величины напрямую зависит динамика разгона и наибольшая скорость, которую способен достигнуть автомобиль;
При этом от его величины напрямую зависит динамика разгона и наибольшая скорость, которую способен достигнуть автомобиль;
• Различные вариации передаточного числа означают еще и частоту, с которой приходится переключать передачи в ходе управления автомобилем.
Таким образом, его величина определяет способности двигателя, особенности управления автомобилем и другие важные характеристики.
Рассчитать указанный показатель довольно просто. Как сказано выше, он означает соотношение количества зубьев на ведомом элементе к их числу на ведущем. Следовательно, если ведомый элемент имеет 40 зубьев, а ведущий 20, то передаточное число будет равно 2.
Исходя из величины передаточного числе и основываясь на принципе его действия, происходит разработка двигателей в автомобилях и сельскохозяйственной технике, а также любых других механизмах, которые оснащены коробкой передач.
Поскольку такой показатель имеет принципиальное значение для условий эксплуатации транспортного средства, то его выбор осуществляется с учетом ряда обстоятельств:
— мощность двигателя и особенности его работы;
— параметры используемых колес;
— особенности системы торможения, ее устройство и надежность.
В целом, именно передаточное число предопределяет специфику управления автомашиной.
Расчет передаточного отношения и частоты вращения.
Как рассчитать передаточное отношение шестерен механической передачи.
В этой статье я приведу пример расчета передаточного отншения шестерен разного диаметра, с разным количеством зубьев. Данный расчет применяется в том случае, когда важно определить к примеру скорость вращения вала редуктора при известной скорости привода и характеристиках зубьев.
Естественно, можно произвести замеры частоты вращения выходного вала, однако в некоторых случаях требуется именно расчет. Помимо этого, в теоретической механике, при конструировании различных узлов и механизмов требуется рассчитать шестерни, чтобы получить заданную скорость вращения.
Помимо этого, в теоретической механике, при конструировании различных узлов и механизмов требуется рассчитать шестерни, чтобы получить заданную скорость вращения.
Термин передаточное число является весьма неоднозначным. Он перекликается с термином передаточное отношение, что не совсем верно. Говоря о передаточном числе, мы подразумеваем сколько оборотов совершит ведомое колесо (шестерня) относительно ведущего.
Для правильного понимания процессов и строения шестерни – следует предварительно ознакомится с ГОСТ 16530-83.
Итак, рассмотрим пример расчета с использованием двух шестерен.
Чтобы рассчитать передаточное отношение мы должны иметь как минимум две шестерни. Это называется зубчатая передача. Обычно первая шестерня является ведущей и находится на валу привода, вторая шестерня называется ведомой и вращается входя в зацепление с ведущей. Пи этом между ними может находится множество других шестерен, которые называются промежуточными. Для упрощения расчета рассмотрим зубчатую передачу с двумя шестернями.
В примере мы имеем две шестерни: ведущую (1) и ведомую (2). Самый простой способ заключается в подсчете количества зубьев на шестернях. Посчитаем количество зубьев на ведущей шестерне. Так же можно посмотреть маркировку на корпусе шестерни.
Представим, что ведущая шестерня (красная) имеет 40 зубьев, а ведомая(синяя) имеет 60 зубьев.
Разделим количество зубьев ведомой шестерни на количество зубьев ведущей шестерни, чтобы вычислить передаточное отношение. В нашем примере: 60/40 = 1,5. Вы также можете записать ответ в виде 3/2 или 1,5:1.
Такое передаточное отношение означает, что красная, ведущая шестерня должна совершить полтора оборота, чтобы синяя, ведомая шестерня совершила один оборот.
Теперь усложним задачу, используя большее количество шестерен. Добавим в нашу зубчатую передачу еще одну шестерню с 14 зубьями. Сделаем ее ведущей.
Начнем с желтой, ведущей шестерни и будем двигаться в направлении ведомой шестерни. Для каждой пары шестерен рассчитываем свое передаточное отношение. У нас две пары: желтая-красная; красная-синяя. В каждой паре рассматриваем первую шестерню как ведущую, а вторую как ведомую.
Для каждой пары шестерен рассчитываем свое передаточное отношение. У нас две пары: желтая-красная; красная-синяя. В каждой паре рассматриваем первую шестерню как ведущую, а вторую как ведомую.
В нашем примере передаточные числа для промежуточной шестерни: 40/14 = 2,9 и 60/40 = 1,5.
Умножаем значения передаточных отношений каждой пары и получаем общее передаточное отношение зубчатой передачи: (20/7) × (30/20) = 4,3. То есть для вычисления передаточного отношения всей зубчатой передачи необходимо перемножить значения передаточных отношений для промежуточных шестерен.
Определим теперь частоту вращения.
Используя передаточное отношение и зная частоту вращения желтой шестерни, можно запросто вычислить частоту вращения ведомой шестерни. Как правило, частота вращения измеряется в оборотах в минуту (об/мин) Рассмотрим пример зубчатой передачи с тремя шестернями. Предположим, что частота вращения желтой шестерни 340 оборотов в минуту. Вычислим частоту вращения красной шестерни.
Будем использовать формулу: S1 × T1 = S2 × T2,
Где:
S1 – частота вращения желтой (ведущей) шестерни,
Т1 – количество зубьев желтой (ведущей) шестерни;
S2- частота вращения красной шестерни,
Т2 – количество зубьев красной шестерни.
В нашем случае нужно найти S2, но по этой формуле вы можете найти любую переменную.
340 rpm × 7 = S2 × 40
2 380 =S2 × 40
2 380 \ 40 = S2
59,5 об/мин = S2
Получается, если ведущая, желтая шестерня вращается с частотой 340 об/мин, тогда ведомая, красная шестерня будет вращаться со скоростью примерно 60 об/мин. Таким же образом рассчитываем частоту вращения пары красная-синяя. Полученный результат – частота вращения синей шестерни – будет являться искомой частотой вращения всей зубчатой передачи.
Как рассчитать передаточное число
Обновлено 9 ноября 2018 г.
Крис Дезиел
Шестерни можно найти практически везде. Они есть в автомобилях, и в трансмиссии, и в дворниках. Они есть в велосипедах, в такой кухонной утвари, как взбиватель для яиц, и даже в часах — по крайней мере, они были раньше. Шестерня представляет собой набор зубчатых колес, соединенных вместе для увеличения или уменьшения скорости вращения приводного вала двигателя.
Они есть в велосипедах, в такой кухонной утвари, как взбиватель для яиц, и даже в часах — по крайней мере, они были раньше. Шестерня представляет собой набор зубчатых колес, соединенных вместе для увеличения или уменьшения скорости вращения приводного вала двигателя.
Величина, на которую зубчатая передача может изменять скорость вращения, зависит от относительных размеров зубчатых колес и называется передаточным числом.Формула передаточного числа оказывается довольно простой. Вы в основном подсчитываете количество зубьев на ведомом колесе и делите его на количество зубьев на ведущем колесе, которое прикреплено к двигателю. Это простой расчет, даже если система передач состоит из нескольких промежуточных колес, называемых холостыми.
Легче рассчитать передаточное число, чем вы думаете
Когда вы соединяете две шестерни, их относительные размеры определяют, насколько быстро каждая из них будет вращаться.Если ведущее колесо меньше ведомого, оно будет вращаться чаще, чем большее. Если ведущее колесо больше, ведомое колесо будет вращаться быстрее.
Вы можете рассчитать величину ускорения и замедления, которую производит простая зубчатая передача, сравнивая радиусы колес, но есть более простой способ. Поскольку зубья обоих шестерен блокируются, они должны быть одинакового размера на обоих колесах, поэтому вы можете просто сравнить количество зубьев на двух колесах.Именно так вы рассчитываете передаточное число. Вы подсчитываете количество зубьев как на ведущем, так и на ведомом колесах и выражаете эти числа в виде отношения или дроби.
Например, если у ведущего колеса 20 зубьев, а у ведомого — 40, вычислите передаточное число как 40/20, что упрощается до 2/1 или 2: 1. (Число зубьев на ведомом колесе всегда идет вверху дроби или первым в соотношении). Это говорит о том, что за каждый оборот ведомого колеса ведущее колесо делает два оборота.Точно так же соотношение 1/2 говорит вам, что ведомое колесо вращается дважды за каждый оборот ведущего колеса — другими словами, ведомое колесо вращается быстрее, чем вал двигателя.
Как применить уравнение передаточного числа к сложным системам
Многие системы зубчатых передач включают в себя одно или несколько промежуточных колес, которые часто используются для обеспечения того, чтобы ведущее и ведомое колеса вращались в одном направлении или для изменения плоскости вращения. Вы можете применить формулу передаточного числа к каждой паре колес в системе передач последовательно, чтобы получить окончательное передаточное число для системы, но вам не нужно этого делать.Если вы это сделаете, вы обнаружите, что произведение всех передаточных чисел совпадает с соотношением между ведущим колесом и ведомым колесом.
Другими словами, ведущее колесо и ведомое колесо — единственные два, которые имеют значение. Независимо от того, сколько холостых колес в системе, конечное передаточное число — это соотношение между ведущим колесом и ведомым колесом. Это верно для всех типов шестерен, включая прямозубые, конические и червячные.
Использование передаточного числа для расчета скорости
Если вам известна скорость вращения ведущего колеса, которая обычно измеряется в оборотах в минуту (об / мин), передаточное число сообщает вам скорость ведомого колеса.Например, рассмотрим систему с передаточным числом 3: 1, что означает, что ведущее колесо вращается в три раза быстрее, чем ведомое. Если скорость ведущего колеса составляет 300 об / мин, скорость ведомого колеса составляет 100 об / мин.
Как правило, вы можете рассчитать скорость вращения, используя следующее уравнение передаточного числа:
S 1 • T 1 = S 2 • T 2 , где
S 1 — это скорость ведущее колесо, а T 1 — количество зубьев на этом колесе.
S 2 и T 2 — скорость и количество зубьев ведомого колеса.
Если вы разрабатываете систему передач, вам пригодится таблица передаточных чисел. Вы можете найти обороты двигателя в технических характеристиках и использовать диаграмму для разработки системы зубчатых передач, которая будет обеспечивать любую требуемую скорость вращения ведомого колеса.
Вы можете найти обороты двигателя в технических характеристиках и использовать диаграмму для разработки системы зубчатых передач, которая будет обеспечивать любую требуемую скорость вращения ведомого колеса.
Шаги для расчета передаточного числа — Блог CLR
Использование шестерен во множестве машин и устройств в настоящее время требует их использования с максимальной эффективностью, чтобы максимально использовать их преимущества.
Одна из ключевых концепций для их надлежащего использования — это передаточное число (r t ). Правильный выбор передаточного числа важен, чтобы:
- Зубчатая передача могла выдерживать больший крутящий момент , минимизируя ошибки.
- Движение может быть создано таким образом, что крутящий момент мотор-шестерни преодолевает инерцию шестерни.
Ниже мы познакомимся с формулами, необходимыми для расчета передаточного числа , а также с тем, что следует учитывать при этом расчете.
Передаточное отношение важно для движения и для того, чтобы шестерня могла выдерживать крутящий момент, не приводя к ошибкам.
Что такое передача движения?
Передаточное число в трансмиссии — это соотношение между скоростями вращения двух зацепляющихся шестерен.
Поскольку каждая шестерня имеет разный диаметр, каждая из осей вращается с разной скоростью, когда они обе включены. Изменение передаточного числа эквивалентно изменению прилагаемого крутящего момента .
Передаточное число рассчитывается путем деления выходной скорости на входную скорость (i = Ws / We) или путем деления количества зубьев ведущей шестерни на количество зубьев ведомой шестерни (i = Ze / Zs).
i = Ws / We
i = Ze / Zs
Преимущества редукторных передач
Редукторные передачи обладают рядом преимуществ по сравнению с другими типами передач.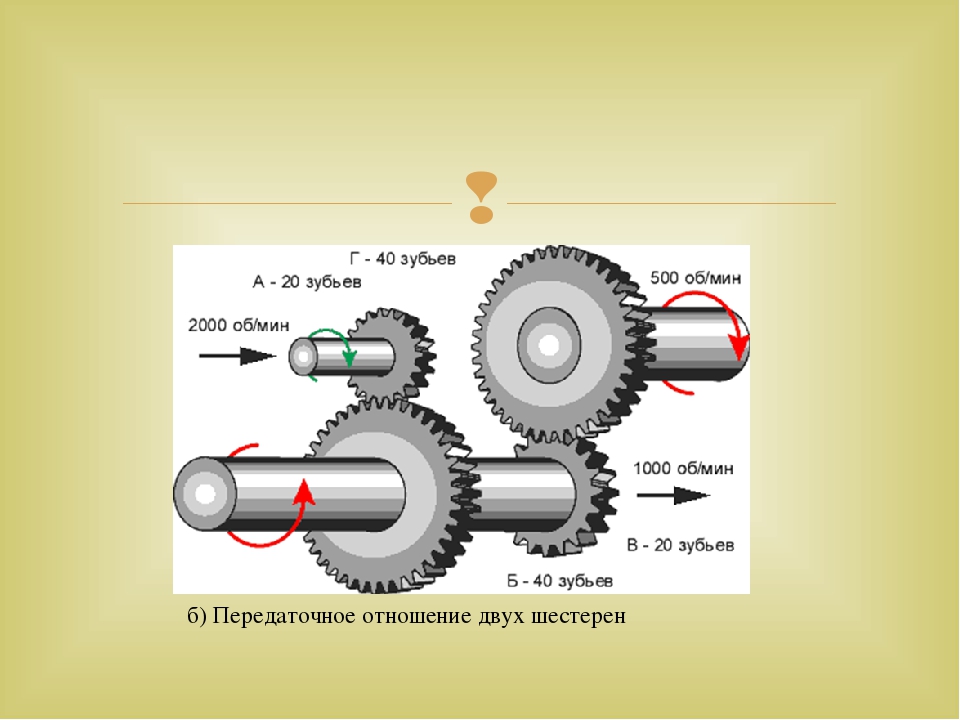 Во-первых, они предлагают высокую производительность при передаче усилий и движений , с длительным сроком службы и высокой надежностью.
Во-первых, они предлагают высокую производительность при передаче усилий и движений , с длительным сроком службы и высокой надежностью.
Но то, что отличает их от других, — это потрясающая точность передаточного числа, что означает, что они могут использоваться в точном оборудовании .
Передаточное число в зубчатых передачах очень точное, что делает эти трансмиссии идеальными для точного машиностроения
В отличие от других механизмов, таких как цепи или шкивы, их размер небольшой , что означает, что они могут быть установлены как в маленькие и большие машины и помещения, а также в труднодоступных местах.
Кроме того, их простое обслуживание делает редукторные трансмиссии одной из самых распространенных систем в основных отраслях промышленности, таких как автомобилестроение.
Параметры для проектирования зубчатой передачи
При проектировании зубчатой передачи необходимо учитывать следующие параметры:
Закон зацепления
Закон зацепления определяет ситуацию, при которой точка контакта между два зубца всегда будут пересекать точку O , если это позволяет их профиль.
Эта точка O должна быть расположена на линии, которая соединяет как центр вращения одной из шестерен, так и центр вращения другой .
Кроме того, радиусы тангажа и расстояния между точкой O и соответствующими центрами должны совпадать.
Передаточное число
Передаточное число ( r t ) — это передаточное число между скоростями вращения двух сопряженных шестерен .
Более конкретно, это частное входной и выходной скоростей ( r t = ω s / ω e ).
Система может вызвать уменьшение , если передаточное число меньше 1, или умножение , если оно больше 1.
Возможно, вас заинтересует: Приводы с регулируемой скоростью: все, что вам нужно знать о редукторах скорости
Коэффициент контакта
Коэффициент контакта ( ε ) измеряет среднее количество зубьев , находящихся в постоянном контакте .
Наилучшее соотношение контактов должно быть больше 1,2, чтобы гарантировать способность передавать высокие нагрузки. , обеспечивает жесткость трансмиссии и обеспечивает бесшумную и равномерную работу.
Как рассчитать передаточное число
Вычислить передаточное число можно несколькими способами. Например:
Расчет передаточного числа конических шестерен
При обращении к коническим зубчатым колесам необходимо учитывать, что оно будет эквивалентно количеству зубьев ведущей шестерни, деленному на число зубьев ведомой шестерни. ( RT = Z1 / Z2 ).
Возможно, вас заинтересует: Расчет шестерен: повышение эффективности ваших трансмиссий.
Расчет передаточного числа зубчатой передачи
В случае зубчатой передачи с двумя шестернями нам необходимо выполнить следующие шаги:
- Подсчитать количество зубьев . Для начала нам нужно будет посчитать количество зубьев ведущей шестерни и количество зубьев ведомой шестерни.
- Разделите количество зубьев ведомой шестерни на количество зубьев ведущей шестерни .В результате получится число раз, которое ведомая меньшая шестерня должна будет повернуться, чтобы большая шестерня совершила один полный оборот.
Передаточное число будет равно количеству зубьев ведущей шестерни, разделенному на количество зубьев ведомой шестерни.
В случае зубчатой передачи с более чем двумя шестернями нам нужно будет выполнить следующие шаги:
- Определить, какая шестерня является ведущей, а какая ведомой, и разделить количество зубьев шестерни.
 бывший и последний .Промежуточная передача никак не повлияет на передаточное число зубчатой передачи.
бывший и последний .Промежуточная передача никак не повлияет на передаточное число зубчатой передачи. - Выполните те же шаги , что и для определения передаточного числа двухступенчатой зубчатой передачи.
Существует множество способов расчета передаточного числа, в зависимости от того, являются ли зубчатые колеса коническими или зубчатыми передачами с двумя или более зубчатыми колесами и т. Д.
Расчет передаточного числа зубчатых колес и цепи
Этот тип Трансмиссии образуют две шестерни и цепь шарнирно-сочлененных звеньев .В нем шестерни вращаются в одном направлении.
Используется для передачи движения между удаленными параллельными валами .
Передаточное число является результатом деления количества зубьев ведущей шестерни и количества зубьев ведомой шестерни .
Вам нужна помощь в расчете передаточного числа ваших редукторных трансмиссий? Не стесняйтесь обращаться к нам, и мы поможем запустить ваш проект и рассчитаем ваши параметры.
Определение передаточного числа
Какое передаточное число?
Коэффициент заемного капитала — это финансовый коэффициент, который сравнивает некоторую форму собственного капитала (или капитала) владельца с заемными средствами или заемными средствами компании.Заработок — это измерение финансового рычага предприятия, которое демонстрирует степень, в которой деятельность фирмы финансируется за счет средств акционеров по сравнению с средствами кредитора.
Коэффициент заемного капитала — это показатель финансового рычага, который демонстрирует степень, в которой деятельность фирмы финансируется за счет собственного капитала по сравнению с долговым финансированием.
Ключевые выводы:
- Коэффициенты заемного капитала — это группа финансовых показателей, которые сравнивают собственный капитал с долгом компании различными способами для оценки размера левериджа и финансовой устойчивости компании.

- Заработок — это показатель того, какая часть операций компании финансируется за счет заемных средств по сравнению с финансированием, полученным от акционеров в качестве капитала.
- Передаточные числа имеют большее значение при сравнении с передаточными числами других компаний в той же отрасли.
Общие сведения о передаточных числах
Наиболее известные примеры передаточных чисел включают:
Взаимодействие с другими людьми Отношение заемного капитала к собственному знак равно Общая задолженность Общий капитал \ begin {выровнен} & \ text {Отношение долга к собственному капиталу} = \ frac {\ text {Общий долг}} {\ text {Общий капитал}} \\ \ end {выровнен} Отношение долга к собственному капиталу = Общий капитал
Взаимодействие с другими людьми Количество начисленных процентов * знак равно EBIT Итого проценты \ begin {выровненный} & \ text {раз заработанный процент *} = \ frac {\ text {EBIT}} {\ text {общий процент}} \\ \ end {выровнен} Количество заработанных процентов * = Общий процент EBIT
Взаимодействие с другими людьми Коэффициент собственного капитала знак равно Капитал Ресурсы \ begin {align} & \ text {Equity Ratio} = \ frac {\ text {Equity}} {\ text {Assets}} \\ \ end {align} Коэффициент собственного капитала = Активы
Взаимодействие с другими людьми Коэффициент задолженности знак равно Общая задолженность Итого Активы \ begin {align} & \ text {Debt Ratio} = \ frac {\ text {Total Debt}} {\ text {Total Assets}} \\ \ end {align} Коэффициент долга = Общая сумма активов
* раз заработанные проценты
Более высокий коэффициент заемных средств указывает на то, что компания имеет более высокий уровень финансового рычага и более восприимчива к спадам в экономике и экономическому циклу.Это связано с тем, что компании с более высоким уровнем левериджа имеют более высокие суммы долга по сравнению с собственным капиталом. Компании с высоким коэффициентом заемных средств имеют более высокие суммы долга к обслуживанию, в то время как компании с более низким расчетным коэффициентом заемных средств имеют больший капитал, на который можно полагаться при финансировании.
Передаточные числа полезны как для внутренних, так и для внешних сторон. При принятии решения о выдаче ссуды финансовые учреждения используют расчет коэффициента заемного капитала. Кроме того, кредитные соглашения могут требовать, чтобы компании действовали в соответствии с указанными руководящими принципами в отношении расчета приемлемого коэффициента заемного капитала.В качестве альтернативы внутреннее руководство использует коэффициенты заемного капитала для анализа будущих денежных потоков и кредитного плеча.
Интерпретация передаточных чисел
Высокий коэффициент заемного капитала обычно указывает на высокую степень левериджа, хотя это не всегда означает, что компания находится в плохом финансовом состоянии. Вместо этого компания с высоким коэффициентом заемных средств имеет более рискованную структуру финансирования, чем компания с более низким коэффициентом заемных средств.
Регулируемые организации обычно имеют более высокие коэффициенты заемного капитала, поскольку они могут работать с более высокими уровнями долга.Кроме того, компании, находящиеся в монополистической ситуации, часто работают с более высокими коэффициентами заемных средств, поскольку их стратегическая маркетинговая позиция снижает риск дефолта. Наконец, отрасли, в которых используются дорогие основные фонды, обычно имеют более высокий коэффициент заемных средств, поскольку эти основные фонды часто финансируются за счет заемных средств.
Передаточное отношение одной фирмы следует сравнивать с пайками других компаний той же отрасли.
Пример использования передаточных чисел
Предположим, что коэффициент долга компании равен 0.6. Хотя эта цифра сама по себе дает некоторую информацию о финансовой структуре компании, более целесообразно сопоставить эту цифру с другой компанией в той же отрасли.
Например, предположим, что коэффициент долга компании в прошлом году составлял 0,3, среднее значение по отрасли — 0,8, а коэффициент долга основного конкурента компании составляет 0,9. Больше информации можно получить из сравнения передаточных чисел друг с другом. Когда результат среднего отраслевого отношения равен 0,8, а результат передаточного отношения конкурента равен 0.9, компания с коэффициентом 0,3 относительно хорошо работает в своей отрасли.
Больше информации можно получить из сравнения передаточных чисел друг с другом. Когда результат среднего отраслевого отношения равен 0,8, а результат передаточного отношения конкурента равен 0.9, компания с коэффициентом 0,3 относительно хорошо работает в своей отрасли.
Как работают передаточные числа | HowStuffWorks
Если вы хотите создать высокое передаточное число, ничто не сравнится с червячной передачей . В червячной передаче вал с резьбой входит в зацепление с зубьями шестерни. Каждый раз, когда вал совершает один оборот, шестерня перемещается на один зуб вперед. Если шестерня имеет 40 зубьев, передаточное число передаточного числа 40: 1 в очень маленьком корпусе. Вот один из примеров стеклоочистителя.
Этот контент несовместим с этим устройством.
Механический одометр — это еще одно место, где используется много червячных передач:
Планетарные передачи
Есть много других способов использования шестерен. Одна специализированная зубчатая передача называется планетарной зубчатой передачей . Планетарные передачи решают следующую проблему. Допустим, вам нужно передаточное число 6: 1, при котором входной сигнал вращается в том же направлении, что и выходной. Один из способов создать это передаточное число — использовать следующую трехступенчатую передачу:
В этой цепочке синяя шестерня в шесть раз больше диаметра желтой шестерни (что дает передаточное число 6: 1).Размер красной шестерни не важен, потому что она просто меняет направление вращения, чтобы синяя и желтая шестерни вращались одинаково. Однако представьте, что вы хотите, чтобы ось выходной шестерни была такой же, как и у входной шестерни. Обычное место, где требуется возможность такой же оси, — это электрическая отвертка. В этом случае вы можете использовать планетарную передачу, как показано здесь:
В этой системе передач желтая передача (солнце ) включает все три красные передачи (планеты ) одновременно. Все три прикреплены к пластине (водило ), и они входят в зацепление с внутри синей шестерни (кольцо ), а не снаружи. Поскольку вместо одной красные шестерни используются три, эта зубчатая передача чрезвычайно прочная. Выходной вал прикреплен к синей коронной шестерне, а водило планетарной передачи удерживается неподвижно — это дает то же передаточное число 6: 1. Вы можете увидеть изображение двухступенчатой планетарной передачи на странице электрической отвертки и трехступенчатой планетарной системы на странице спринклерных систем.Внутри автоматических трансмиссий вы также найдете планетарные передачи.
Все три прикреплены к пластине (водило ), и они входят в зацепление с внутри синей шестерни (кольцо ), а не снаружи. Поскольку вместо одной красные шестерни используются три, эта зубчатая передача чрезвычайно прочная. Выходной вал прикреплен к синей коронной шестерне, а водило планетарной передачи удерживается неподвижно — это дает то же передаточное число 6: 1. Вы можете увидеть изображение двухступенчатой планетарной передачи на странице электрической отвертки и трехступенчатой планетарной системы на странице спринклерных систем.Внутри автоматических трансмиссий вы также найдете планетарные передачи.
Еще одна интересная особенность планетарных редукторов заключается в том, что они могут создавать разные передаточные числа в зависимости от того, какую передачу вы используете в качестве входной, какую передачу вы используете в качестве выхода, а какую вы держите неподвижно. Например, если вход — солнечная шестерня, и мы удерживаем коронную шестерню неподвижно и прикрепляем выходной вал к водилу планетарной передачи, мы получаем другое передаточное число. В этом случае водило планеты и планеты вращаются вокруг солнечной шестерни, поэтому вместо того, чтобы солнечная шестерня должна вращаться шесть раз, чтобы водило планеты совершило один оборот, она должна вращаться семь раз.Это связано с тем, что водило планетарной передачи один раз облетело солнечную шестерню в том же направлении, в котором она вращалась, вычитая один оборот из солнечной шестерни. Таким образом, в этом случае мы получаем сокращение 7: 1.
Вы можете снова переставить все, и на этот раз удерживайте солнечную шестерню неподвижно, снимите выход с водила планетарной передачи и подсоедините вход к коронной шестерне. Это даст вам редуктор 1,17: 1. В автоматической коробке передач используются планетарные редукторы для создания различных передаточных чисел, а также используются муфты и тормозные ленты для удержания различных частей редуктора в неподвижном состоянии и изменения входов и выходов.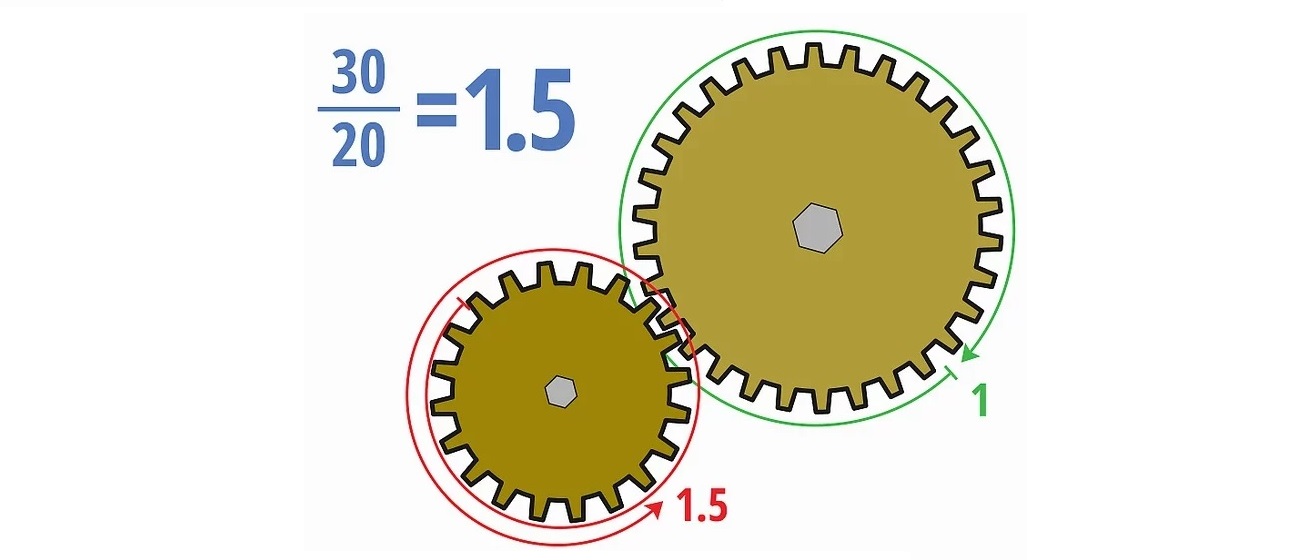
Калькулятор передаточного числа
Этот калькулятор передаточного отношения определяет механическое преимущество, которое дает двухступенчатая установка в машине. Передаточное число дает нам представление о том, насколько выходная шестерня ускоряется или замедляется, или сколько крутящего момента теряется или увеличивается в системе. Мы снабдили этот калькулятор уравнением передаточного числа и уравнением редуктора, чтобы вы могли быстро определить передаточное число ваших шестерен. Чтобы узнать больше о расчете передаточного числа и о том, как это важно при создании простых (и даже сложных) машин, продолжайте читать.
Но сначала: что такое шестерня?
Шестерня — зубчатое колесо, которое может изменять направление, крутящий момент и скорость вращательного движения, приложенного к нему. Шестерни бывают разных форм и размеров, и эти различия описывают поступательное движение или передачу вращательного движения. Передача движения происходит, когда две или более шестерен в системе сцепляются вместе во время движения. Мы называем эту систему зубчатых колес зубчатой передачей .
В зубчатой передаче поворот одной шестерни также приводит к вращению других шестерен.Шестерня, которая изначально получает крутящее усилие либо от мотора с приводом, либо вручную (или ногой в случае велосипеда), называется входной шестерней . Мы также можем назвать это ведущей шестерней, поскольку она инициирует движение всех других шестерен в зубчатой передаче. Последняя шестерня, на которую влияет входная шестерня, известна как выходная шестерня . В двухступенчатой системе мы можем назвать эти шестерни ведущей шестерней и ведомой шестерней соответственно.
Результирующее движение выходной шестерни может быть в том же направлении, что и входная шестерня, но может быть в другом направлении или осях вращения в зависимости от типа шестерен в зубчатой передаче. Чтобы помочь вам это наглядно представить, вот иллюстрация различных типов шестерен и их взаимосвязей между входом и выходом:
Чтобы помочь вам это наглядно представить, вот иллюстрация различных типов шестерен и их взаимосвязей между входом и выходом:
Что такое передаточное число и как рассчитать передаточное число
Передаточное число — это отношение длины окружности входной шестерни к окружности выходной шестерни в зубчатой передаче. Передаточное число помогает нам определить количество зубьев, необходимое каждой шестерне для достижения желаемой выходной скорости / угловой скорости или крутящего момента.
Мы вычисляем передаточное число между двумя шестернями, разделив длину окружности входной шестерни на окружность выходной шестерни.Мы можем определить окружность конкретной шестерни так же, как вычисляем длину окружности. В форме уравнения это выглядит так:
Передаточное число = (π * диаметр входной шестерни) / (π * диаметр выходной шестерни)
Упрощая это уравнение, мы также можем получить передаточное число, когда учитываются только диаметр или радиус шестерен:
-
Передаточное число = (π * диаметр входной шестерни) / (π * выходная шестерня) -
Передаточное число = (диаметр входной шестерни) / (диаметр выходной шестерни) -
Передаточное число = (радиус входной шестерни) / (радиус выходной шестерни)
Точно так же мы можем рассчитать передаточное число, учитывая количество зубьев на входной и выходной шестернях.Это аналогично рассмотрению окружностей шестерен. Мы можем выразить окружность шестерни, умножив сумму толщины зуба и расстояния между зубьями на количество зубьев шестерни:
Передаточное число = (количество зубьев первичной шестерни * (толщина шестерни + расстояние между зубьями)) / (число зубьев вторичной шестерни * (толщина шестерни + расстояние между зубьями))
Но, поскольку толщина и расстояние между зубьями зубчатой передачи должны быть одинаковыми для того, чтобы зубчатые колеса зацепились плавно, мы можем исключить множитель толщины зубчатой передачи и шага зубьев в приведенном выше уравнении, оставив нам следующее уравнение:
Передаточное число = количество зубьев входной шестерни / количество зубьев выходной шестерни
Передаточное число, как и любые другие передаточные числа, может быть выражено как:
- дробь или частное — где, если возможно, мы упрощаем дробь, разделив числитель и знаменатель на их наибольший общий делитель.

- десятичное число — выражение передаточного числа в виде десятичного числа дает нам быстрое представление о том, насколько необходимо повернуть входную шестерню, чтобы выходная шестерня совершила один полный оборот.
- упорядоченная пара чисел , разделенных двоеточием, например 2: 5 или 1:14 . Благодаря этому мы можем увидеть наименьшее количество оборотов, необходимое для одновременного возврата как входной, так и выходной шестерен в исходное положение.
С другой стороны, если мы возьмем обратную величину передаточного числа в ее дробной форме и упростим ее до десятичного числа, мы получим значение механического преимущества (или недостатка) нашей зубчатой передачи или зубчатой системы.
Понимание передаточного числа и значений механического преимущества
Передаточные числа довольно легко понять, и теперь, когда мы знаем, как рассчитать передаточное число, не лучше ли узнать, как оно влияет на сами шестерни? Чтобы лучше объяснить передаточные числа, давайте рассмотрим систему с двумя шестернями, в которой входная и выходная шестерни имеют десять и сорок зубьев соответственно:
Следуя нашему уравнению передаточного числа, мы можем сказать, что эта зубчатая передача имеет передаточное число 10:40, 10/40 или просто 1/4 (или 0.25). Это передаточное число означает, что выходная шестерня будет вращаться только на 1/4 полного оборота после того, как входная шестерня совершит полный оборот. Продолжая в том же духе и сохраняя постоянную входную скорость, мы видим, что выходная шестерня также составляет 1/4 скорости входной скорости. Другими словами, скорость входной шестерни в четыре раза превышает скорость выходной шестерни, как показано на анимированном изображении ниже:
Хотя эта установка демонстрирует редуктор с точки зрения скорости, в свою очередь, он дает нам выход, который имеет на больше крутящего момента по сравнению с входом. Обратное передаточное число составляет 4/1, поэтому мы можем сказать, что мы получаем в четыре раза больше механического преимущества, когда дело касается крутящего момента.
Обратное передаточное число составляет 4/1, поэтому мы можем сказать, что мы получаем в четыре раза больше механического преимущества, когда дело касается крутящего момента.
Важное примечание о промежуточных шестернях
Прямозубая цилиндрическая шестерня с любым числом зубьев между входной и выходной шестернями не изменяет общее передаточное число зубчатой передачи. Однако эта шестерня (или шестерни) может изменять направление выходной шестерни. Мы называем эту промежуточную шестерню промежуточной шестерней. В качестве примера приведем редукторную систему 1: 2,5 с дополнительной промежуточной шестерней:
Без промежуточной шестерни — та же зубчатая передача.Обратите внимание, что направление выходной шестерни обратное:
Реальные простые машины с зубчатыми колесами
Мы видим шестерни в повседневной жизни, и, чтобы лучше понять передаточные числа, вот несколько реальных примеров простых машин с шестернями в них:
Механическое преимущество по скорости
Ручные дрели, хотя они кажутся менее популярными в настоящее время, являются отличным примером простой машины, которая демонстрирует механическое преимущество с точки зрения скорости.Если повернуть ручку, сверло будет вращаться с высокой скоростью.Механическое преимущество по крутящему моменту
Поднимаясь в гору, ехать на велосипеде легче, если вы используете низкоскоростную передачу. Это приводит к лучшему крутящему моменту и большей мощности при движении в гору. Это может означать, что нам придется больше крутить педали, но подъем будет намного легче. Велосипедный цепной механизм очень похож на зубчатую рейку. Цепь действует как реечная передача, напрямую передавая движение на заднюю звездочку велосипеда.Как рассчитать передаточное число? — x-engineer.org
Шестерни являются жизненно важным компонентом машин, робототехники, транспортных средств, аэрокосмической продукции и так далее. Наверное, все, что движется, в каждой машине есть хотя бы одна шестерня.
Наверное, все, что движется, в каждой машине есть хотя бы одна шестерня.
Самым простым применением является редуктор . Это машина, оборудование, которое преобразует входную скорость и крутящий момент в выходную скорость и крутящий момент. Под преобразованием мы подразумеваем усиление или уменьшение . Уровень трансформации задается передаточным числом .
Редуктор — это коробка передач только с одной передачей. Передаточное число получается за счет зацепления двух цилиндрических зубчатых колес .
Изображение: Анимация редуктора (щелкните изображение для анимации)
Редуктор обычно используется в качестве усилителя крутящего момента . Например, вам нужно привести в действие гидравлический насос, которому требуется большое количество крутящего момента. Ваш источник энергии, скажем, электродвигатель. Между мотором и насосом устанавливаем шестеренчатый редуктор.
Как рассчитать передаточное число?
Если вам необходимо увеличить крутящий момент двигателя в 3 раза, то вам понадобится редуктор с коэффициентом 3.0 Передаточное число . Чтобы рассчитать передаточное число двух зубчатых колес с зацеплением, нам необходимо знать:
- количество зубьев как входной, так и выходной шестерни
- базовый диаметр или радиус входной и выходной шестерен
Изображение: Схема сил зубчатой сетки
В таблице ниже у нас есть все физические значения, которые мы собираемся использовать в наших расчетах. Со знаком вопроса (?) У нас есть все переменные, которые нам нужно вычислить.
| Переменная | Описание | Значение | Единица |
| \ [z_ {IN} \] | количество зубьев входной шестерни | 16553 16 | |
| \ [z_ {OUT} \] | количество зубьев ведомой шестерни | 24 | — |
| \ [r_ {IN} \] | радиус основания ведущей шестерни | 80 | мм |
| \ [r_ {OUT} \] | радиус основания выходной шестерни | 120 | мм |
| \ [i \] | передаточное число | ? | — |
| \ [Tq_ {IN} \] | входной крутящий момент | 250 | Нм |
| \ [Tq_ {OUT} \] | выходной крутящий момент | ? | Нм |
| \ [\ omega_ {IN} \] | входная (вращательная) частота вращения | 1500 | об / мин |
| \ [\ omega_ {OUT} \] | выходная (вращательная) частота вращения | ? | об / мин |
| \ [F_ {t} \] | контактная (касательная) сила | (нет необходимости) | N |
| \ [v_ {t} \] | контактная (касательная) скорость | (нет необходимости) | м / с |
Под вводом понимается источник энергии, в нашем случае это может быть электродвигатель.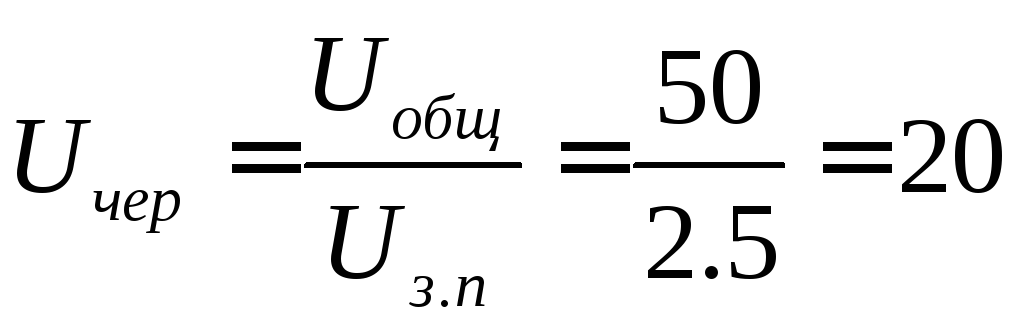 Под мощностью мы подразумеваем, где подается мощность (например, гидравлический насос).
Под мощностью мы подразумеваем, где подается мощность (например, гидравлический насос).
Передаточное число i можно рассчитать двумя способами:
- как отношение числа зубьев ведомой шестерни к числу зубцов ведущей шестерни
- как отношение между базовым радиусом выходной шестерни и базовым радиусом входной шестерни
Базовый радиус измеряется от центра вращения шестерни до точки контакта зубьев.Тот же результат достигается при использовании внешнего радиуса, который проходит от центра шестерни до вершины зубьев.
Заменяя математические выражения на фактическое количество зубьев и радиус, мы получаем передаточное число i :
\ [\ begin {уравнение *} \ begin {split}i & = \ frac {z_ { OUT}} {z_ {IN}} & = \ frac {24} {16} & = 1.5 \\
i & = \ frac {r_ {OUT}} {r_ {IN}} & = \ frac {120} { 80} & = 1,5
\ end {split} \ end {формула *} \]
Соотношение между выходным крутящим моментом и входным крутящим моментом следующее:
\ [\ begin {уравнение *} \ begin {split}Tq_ {OUT} = i \ cdot Tq_ {IN}
\ end {split} \ end {формула *} \]
Зубчатый редуктор будет увеличивать входной крутящий момент в количество раз, равное передаточному отношению:
\ [\ begin { уравнение *} \ begin {split}Tq_ {OUT} = 1.5 \ cdot 250 = 375 \ text {Nm}
\ end {split} \ end {формула *} \]
Соотношение между выходной скоростью и входной скоростью следующее:
\ [\ begin {уравнение *} \ begin {split}\ omega_ {OUT} = \ frac {\ omega_ {IN}} {i}
\ end {split} \ end {формула *} \]
Редуктор уменьшит входную скорость в несколько раз равно передаточному отношению:
\ [\ begin {уравнение *} \ begin {split}\ omega_ {OUT} = \ frac {1500} {1.5} = 1000 \ text {rpm}
\ end {split} \ end {уравнение *} \]
Теперь мы собираемся продемонстрировать, почему значение выходного крутящего момента — это входной крутящий момент, умноженный на передаточное число. Кто придумал эту формулу?
Кто придумал эту формулу?
В точке контакта между зубьями шестерен возникает касательная сила. Эта касательная сила может быть вычислена функцией входной шестерни и функцией выходной шестерни.
Мы знаем, что крутящий момент — это произведение прилагаемой силы на длину плеча рычага. В нашем случае сила — это тангенциальная сила между зубьями, а рычаг — это радиус шестерни.
\ [\ begin {уравнение *} \ begin {split}Tq_ {in} = r_ {IN} \ cdot F_ {t} \\
\ end {split} \ end {уравнение *} \]
Отсюда мы извлеките касательную силу:
\ [\ begin {уравнение *} \ begin {split}F_ {t} = \ frac {Tq_ {IN}} {r_ {IN}}
\ end {split} \ end {уравнение * } \]
Та же сила действует на выходную шестерню:
\ [\ begin {формула *} \ begin {split}F_ {t} = \ frac {Tq_ {OUT}} {r_ {OUT}}
\ end {split} \ end {формула *} \]
Соединяя два математических выражения тангенциальной силы, мы получаем:
\ [\ begin {equal *} \ begin {split}\ frac {Tq_ {OUT} } {r_ {OUT}} & = \ frac {Tq_ {IN}} {r_ {IN}} \\
Tq_ {OUT} & = \ frac {r_ {OUT}} {r_ {IN}} \ cdot Tq_ { IN} \\
Tq_ {OUT} & = i \ cdot Tq_ {IN}
\ end {split} \ end {формула *} \]
Теперь давайте продемонстрируем влияние передаточного числа на выходную скорость.Мы используем то же изображение, что и выше, но с обозначениями скорости вместо сил.
Изображения: Схема скоростей зубчатого зацепления
Тангенциальная скорость одинакова в точке контакта двух шестерен. В качестве тангенциальной силы мы можем записать функцию тангенциальной скорости входной шестерни и выходной шестерни:
Мы знаем, что тангенциальная скорость — это произведение радиуса на скорость вращения.
\ [\ begin {уравнение *} \ begin {split}v_ {t} = \ omega_ {IN} \ cdot r_ {IN}
\ end {split} \ end {уравнение *} \]
Такая же скорость применяется на выходной шестерне:
\ [\ begin {формула *} \ begin {split}v_ {t} = \ omega_ {OUT} \ cdot r_ {OUT}
\ end {split} \ end {формула *} \ ]
Соединяя два математических выражения тангенциальной скорости, мы получаем:
\ [\ begin {уравнение *} \ begin {split}\ omega_ {OUT} \ cdot r_ {OUT} & = \ omega_ {IN} \ cdot r_ {IN} \\
\ omega_ {OUT} & = \ frac {r_ {IN}} {r_ {OUT}} \ cdot \ omega_ {IN} \\
\ omega_ {OUT} & = \ frac { \ omega_ {IN}} {i}
\ end {split} \ end {формула *} \]
К концу этого урока вы должны знать, как рассчитать функцию передаточного числа шестерен, а также влияние шестерни. соотношение по крутящему моменту и скорости.
соотношение по крутящему моменту и скорости.
Для любых вопросов или замечаний относительно этого руководства, пожалуйста, используйте форму комментариев ниже.
Не забывайте ставить лайки, делиться и подписываться!
Передаточное число — Энциклопедия Нового Света
Передаточное число на сельскохозяйственном оборудовании, передаточное число 1: 1,62Передаточное число — это соотношение между количеством зубьев на двух шестернях, которые находятся в зацеплении, или двух звездочек, соединенных общей роликовой цепью, или окружностями двух шкивов, соединенных приводным ремнем.
Звездочка и роликовая цепь.Общее описание
На рисунке справа меньшая шестерня (известная как ведущая шестерня) имеет 13 зубцов, а вторая, более крупная шестерня (известная как промежуточная шестерня) имеет 21 зуб. Таким образом, передаточное число составляет 13/21 или 1 / 1,62 (также записывается как 1: 1,62).
Это означает, что за каждый оборот шестерни шестерня совершает 1 / 1,62 или 0,62 оборота. На практике передача крутится медленнее.
Предположим, что самая большая шестерня на картинке имеет 42 зубца, таким образом, передаточное число между второй и третьей шестернями составляет 21/42 = 1/2, и за каждый оборот самой маленькой шестерни самая большая шестерня повернулась только на 0.62/2 = 0,31 оборота, общее уменьшение примерно 1: 3,23.
Поскольку промежуточная шестерня (промежуточная шестерня) контактирует напрямую как с меньшей, так и с большой шестерней, ее можно исключить из расчета, что также дает соотношение 42/13 = 3,23.
Поскольку количество зубьев также пропорционально окружности зубчатого колеса (чем больше колесо, тем больше у него зубьев), передаточное число также может быть выражено как отношение между окружностями обоих колес (где d — диаметр меньшего колеса, а D — диаметр большего колеса):
- gr = πdπD = dD {\ displaystyle gr = {\ frac {\ pi d} {\ pi D}} = {\ frac {d} {D}}}
Поскольку диаметр равен удвоенному радиусу ;
- gr = dD = 2r2R = rR {\ displaystyle gr = {\ frac {d} {D}} = {\ frac {2r} {2R}} = {\ frac {r} {R}}}
также.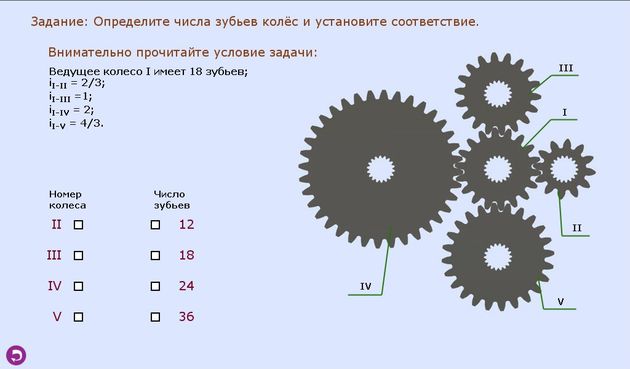
- vd = vD → ωdr = ωDR → rR = ωDωd {\ displaystyle v_ {d} = v_ {D} \ rightarrow \ omega _ {d} r = \ omega _ {D} R \ rightarrow {\ frac {r} {R}} = {\ frac {\ omega _ {D}} {\ omega _ {d}}}}
и т. Д.
- gr = ωDωd {\ displaystyle gr = {\ frac {\ omega _ {D}} {\ omega _ {d}}}}
Другими словами, передаточное число пропорционально соотношению диаметров шестерен и обратно пропорционально соотношению скоростей передачи.
Ремни также могут иметь зубья и соединяться с зубчатыми шкивами.Специальные шестерни, называемые звездочками, могут соединяться вместе с цепями, как на велосипедах и некоторых мотоциклах. Опять же, с этими машинами можно вести точный учет зубьев и оборотов.
Шестерни газораспределения на двигателе Ford Taunus V4 — малая шестерня находится на коленчатом валу, большая шестерня — на распредвале. Шестерня коленчатого вала имеет 34 зуба, шестерня распределительного вала — 68 зубцов и работает на половине частоты вращения коленчатого вала.(Маленькая шестерня в левом нижнем углу находится на балансирном валу.)
Ремень с зубьями, называемый зубчатым ремнем, используется в некоторых двигателях внутреннего сгорания для точной синхронизации движения распределительного вала с движением коленчатого вала, так что клапаны открываются и закрываются в верхней части каждого цилиндра точно в нужное время. относительно движения каждого цилиндра.С момента съезда автомобиля со стоянки до момента, когда потребуется замена ремня через тысячи километров, он точно синхронизирует два вала. На некоторых автомобилях для этой цели используется цепь, называемая цепью привода ГРМ, в то время как в других распределительный вал и коленчатый вал соединяются напрямую через зацепленные шестерни. Но какая бы форма привода ни использовалась, в четырехтактных двигателях передаточное отношение коленчатого вала к распределительному валу всегда составляет 2: 1, что означает, что за каждые два оборота коленчатого вала распределительный вал будет совершать один оборот.
Автомобильные трансмиссии обычно имеют две или более области, в которых используется передача: одна в трансмиссии, которая содержит ряд различных наборов передач, которые могут быть изменены для обеспечения широкого диапазона скоростей транспортного средства, а другая — в дифференциале, который содержит один дополнительный набор зубчатых колес, который обеспечивает дополнительное механическое преимущество на колесах. Эти компоненты могут быть отдельными и соединены приводным валом, или они могут быть объединены в один блок, называемый трансмиссией.
Шевроле Корвет C5 Z06 2004 года выпуска с шестиступенчатой механической коробкой передач имеет следующие передаточные числа в трансмиссии:
| Шестерня | Коэффициент |
|---|---|
| 1-я передача | 2.97: 1 |
| 2-я передача | 2,07: 1 |
| 3-я передача | 1,43: 1 |
| 4-я передача | 1,00: 1 |
| 5-я передача | 0,84: 1 |
| 6-я передача | 0,56: 1 |
| обратный | 3,28: 1 |
На 1-й передаче двигатель делает 2,97 оборота на каждый оборот выходной мощности трансмиссии. На 4-й передаче передаточное число 1: 1 означает, что двигатель и трансмиссия движутся с одинаковой скоростью.5-я и 6-я передачи известны как повышающие передачи, в которых выходной сигнал трансмиссии вращается быстрее, чем двигатель.
У указанного выше Corvette передаточное число дифференциала составляет 3,42: 1. Это означает, что на каждые 3,42 оборота выхода трансмиссии колеса совершают один оборот. Передаточное число дифференциала умножается на передаточное число, поэтому на 1-й передаче двигатель делает 10,16 оборотов за каждый оборот колес.
Шины автомобиля можно рассматривать как третий тип зубчатой передачи.Примерный Corvette Z06 оснащен шинами 233 / 45-14, которые имеют окружность 82,1 дюйма. Это означает, что за каждый полный оборот колеса автомобиль проходит 82,1 дюйма. Если бы у Corvette были шины большего размера, он бы путешествовал дальше с каждым оборотом колеса, что было бы похоже на более высокую передачу. Если бы у автомобиля были шины меньшего размера, это было бы похоже на более низкую передачу.
Это означает, что за каждый полный оборот колеса автомобиль проходит 82,1 дюйма. Если бы у Corvette были шины большего размера, он бы путешествовал дальше с каждым оборотом колеса, что было бы похоже на более высокую передачу. Если бы у автомобиля были шины меньшего размера, это было бы похоже на более низкую передачу.
Используя передаточные числа трансмиссии и дифференциала, а также размер шин, становится возможным вычислить скорость автомобиля для конкретной передачи при определенных оборотах двигателя.
Например, можно определить расстояние, которое автомобиль пройдет за один оборот двигателя, разделив длину окружности шины на комбинированное передаточное число трансмиссии и дифференциала.
d = ctgrt × grd {\ displaystyle d = {\ frac {c_ {t}} {gr_ {t} \ times gr_ {d}}}}
Можно определить скорость автомобиля по частоте вращения двигателя, умножив длину окружности шины на частоту вращения двигателя и разделив на комбинированное передаточное число.
vc = ct × vegrt × grd {\ displaystyle v_ {c} = {\ frac {c_ {t} \ times v_ {e}} {gr_ {t} \ times gr_ {d}}}}
| Шестерня | дюймов на оборот двигателя | Скорость на 1000 об / мин |
|---|---|---|
| 1-я передача | 8.1 дюйм | 7,7 миль / ч |
| 2-я передача | 11,6 дюймов | 11,0 миль / ч |
| 3-я передача | 16.8 дюймов | 15,9 миль / ч |
| 4-я передача | 24,0 дюйма | 22,7 миль / ч |
| 5-я передача | 28,6 дюймов | 27,1 миль / ч |
| 6-я передача | 42,9 дюйма | 40,6 миль / ч |
Широкое соотношение сторон vs.Редукторная трансмиссия
Коробка передач с близким передаточным числом — это коробка передач, в которой имеется относительно небольшая разница между передаточными числами шестерен. Например, трансмиссия с передаточным отношением вала двигателя к ведущему валу 4: 1 на первой передаче и 2: 1 на второй передаче будет считаться широкой по сравнению с другой трансмиссией с передаточным отношением 4: 1 на первой передаче и 3: 1 в секунду. Это потому, что для первой передачи с широким передаточным числом = 4/1 = 4, второй передачи = 2/1 = 2, поэтому передаточное число трансмиссии = 4/2 = 2 (или 200 процентов).Для первой передачи с близким передаточным числом = 4/1 = 4, второй передачи = 3/1 = 3, поэтому передаточное число трансмиссии = 4/3 = 1,33 (или 133 процента), поскольку 133 процента меньше 200 процентов, трансмиссия с 133-процентным передаточным отношением между передачами считается близким передаточным числом. Однако не все трансмиссии начинаются с одинаковым передаточным числом на 1-й передаче или заканчиваются одинаковым передаточным числом на 5-й передаче, что затрудняет сравнение широкой и закрытой трансмиссий.
Например, трансмиссия с передаточным отношением вала двигателя к ведущему валу 4: 1 на первой передаче и 2: 1 на второй передаче будет считаться широкой по сравнению с другой трансмиссией с передаточным отношением 4: 1 на первой передаче и 3: 1 в секунду. Это потому, что для первой передачи с широким передаточным числом = 4/1 = 4, второй передачи = 2/1 = 2, поэтому передаточное число трансмиссии = 4/2 = 2 (или 200 процентов).Для первой передачи с близким передаточным числом = 4/1 = 4, второй передачи = 3/1 = 3, поэтому передаточное число трансмиссии = 4/3 = 1,33 (или 133 процента), поскольку 133 процента меньше 200 процентов, трансмиссия с 133-процентным передаточным отношением между передачами считается близким передаточным числом. Однако не все трансмиссии начинаются с одинаковым передаточным числом на 1-й передаче или заканчиваются одинаковым передаточным числом на 5-й передаче, что затрудняет сравнение широкой и закрытой трансмиссий.
Коробки передач с близким передаточным числом обычно предлагаются в спортивных автомобилях, в которых двигатель настроен на максимальную мощность в узком диапазоне рабочих скоростей, и можно ожидать, что водитель будет наслаждаться частым переключением передач, чтобы двигатель оставался в своем диапазоне мощности.
Холостые шестерни
Обратите внимание, что в последовательности сцепленных вместе шестерен передаточное число зависит только от количества зубьев на первой и последней шестернях. Промежуточные шестерни, независимо от их размера, не изменяют общее передаточное число цепи. Но, конечно, добавление каждой промежуточной шестерни меняет направление вращения последней шестерни.
Промежуточная шестерня, которая не приводит в движение вал для выполнения какой-либо работы, называется промежуточной шестерней . Иногда одна промежуточная шестерня используется для реверсирования направления, и в этом случае она может упоминаться как обратная промежуточная шестерня .Например, обычная автомобильная механическая трансмиссия включает передачу заднего хода посредством вставки промежуточного колеса заднего хода между двумя передачами.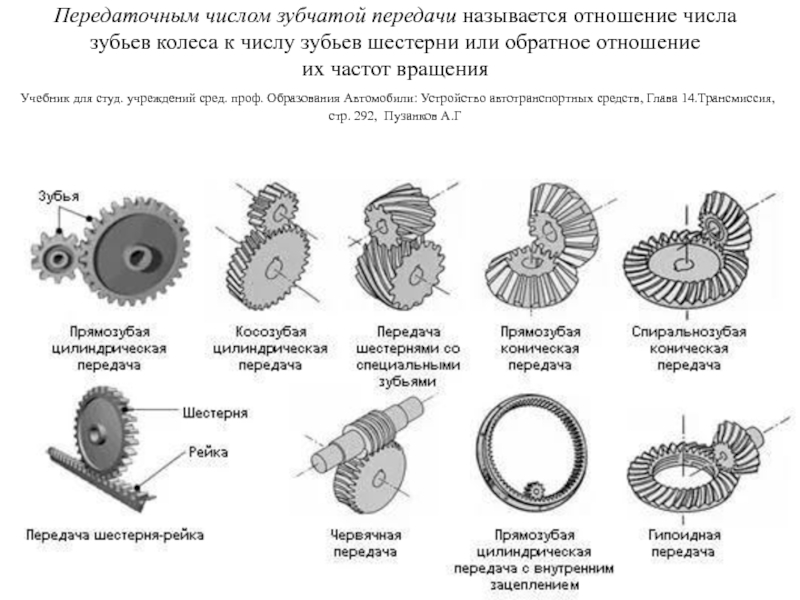
Холостые шестерни могут также передавать вращение между удаленными валами в ситуациях, когда было бы непрактично просто увеличивать удаленные шестерни, чтобы свести их вместе. Шестерни большего размера не только занимают больше места, но и масса и инерция вращения (момент инерции) шестерни квадратичны по длине радиуса. Разумеется, вместо промежуточных шестерен можно использовать зубчатый ремень или цепь для передачи крутящего момента на расстояние.
См. Также
Ссылки
- Букингем, Эрл. 1988. Аналитическая механика зубчатых колес. Springfield, VT: Buckingham Associates. ISBN 0486657124.
- Даути, Вентон Леви и Алекс Валланс. 1964. Конструирование деталей машин, 4-е изд. Нью-Йорк: Макгроу-Хилл. ISBN 0070176353.
- Дадли, Дарл В. 1994. Справочник по практическому проектированию шестерен. Бока-Ратон, Флорида: CRC Press. ISBN 1566762189.
- Хортон, Холбрук и Эрл Бэкингем.1999. Manual of Gear Design Vol. 1-3 Нью-Йорк: Industrial Press. ISBN 0831131160.
- Джонс, Франклин. 1961. Gear Design Simplified, 3-е изд. Нью-Йорк: Промышленная пресса. ISBN 0831111593.
- Энциклопедия науки и техники Макгроу-Хилла. 2002. Нью-Йорк: Макгроу-Хилл. ISBN 0079136656.
Внешние ссылки
Все ссылки получены 24 мая 2017 г.
Кредиты
Энциклопедия Нового Света писатели и редакторы переписали и завершили статью Википедия в соответствии со стандартами New World Encyclopedia .Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с указанием авторства. Кредит предоставляется в соответствии с условиями этой лицензии, которая может ссылаться как на участников Энциклопедии Нового Света, участников, так и на самоотверженных добровольцев Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования.

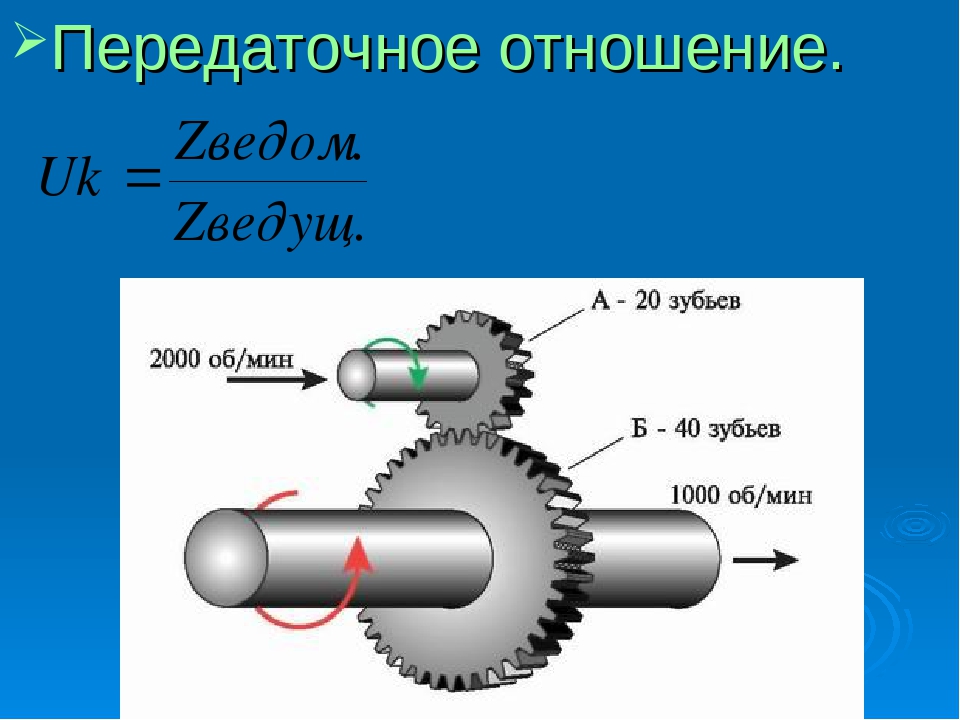 Направление вращения не меняется, если у колеса нарезка зубьев сделана внутри колеса.
Направление вращения не меняется, если у колеса нарезка зубьев сделана внутри колеса.
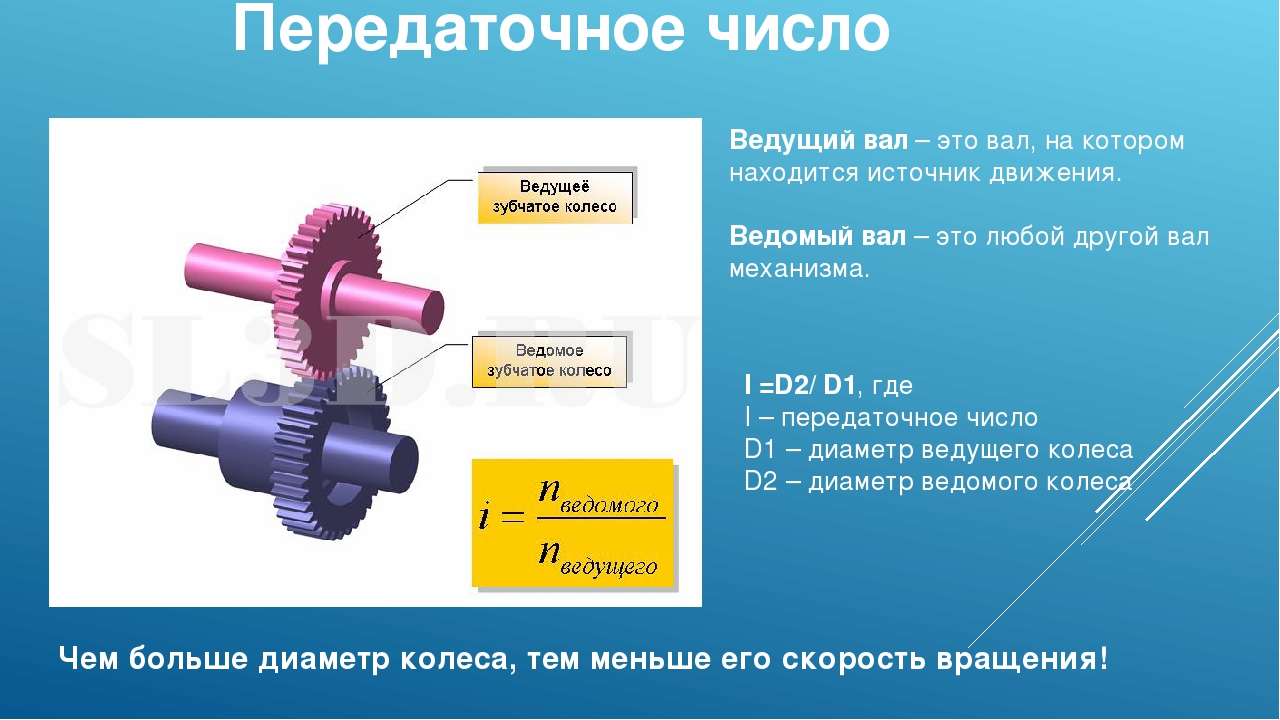 Для этого необходимо покрутить быстроходный вал и количество его оборотов за один оборот тихоходного вала и будет означать фактическое передаточное число.
Для этого необходимо покрутить быстроходный вал и количество его оборотов за один оборот тихоходного вала и будет означать фактическое передаточное число.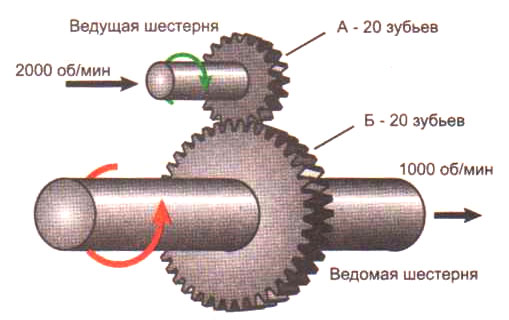 бывший и последний .Промежуточная передача никак не повлияет на передаточное число зубчатой передачи.
бывший и последний .Промежуточная передача никак не повлияет на передаточное число зубчатой передачи.