2.2. Вычисление скоростей точек тела, совершающего плоскопараллельное движение
В любой момент времени скорости
любых двух точек плоской фигуры  и
и связаны равенством
связаны равенством
|
Рис. 2.3 |
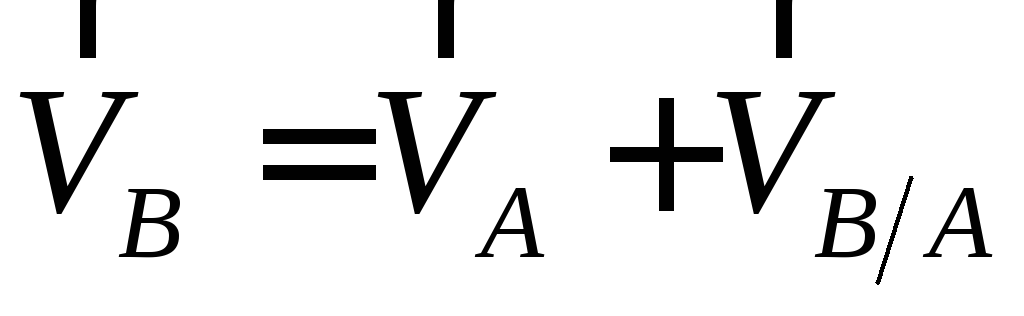 (a)
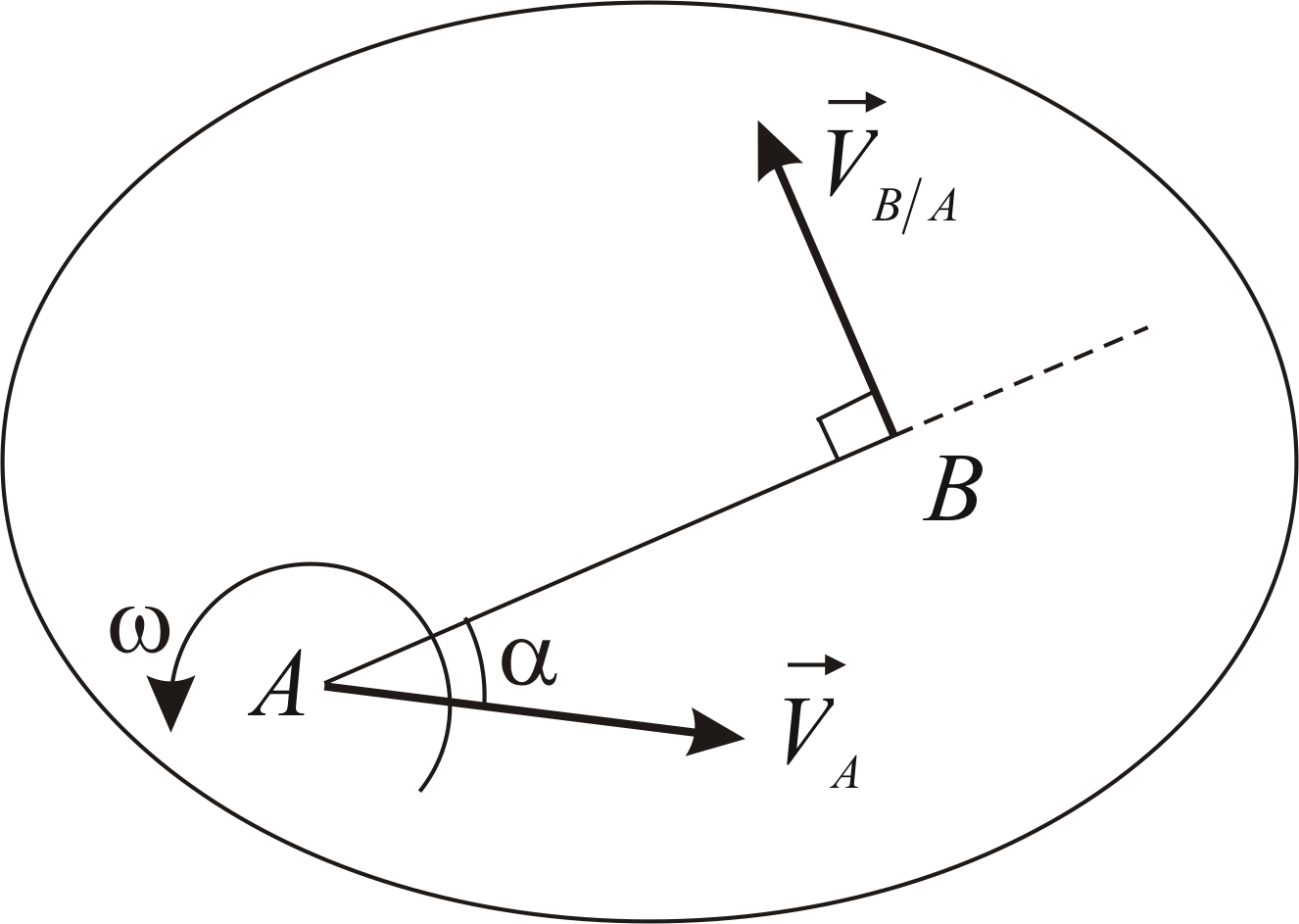
(a) Вектор 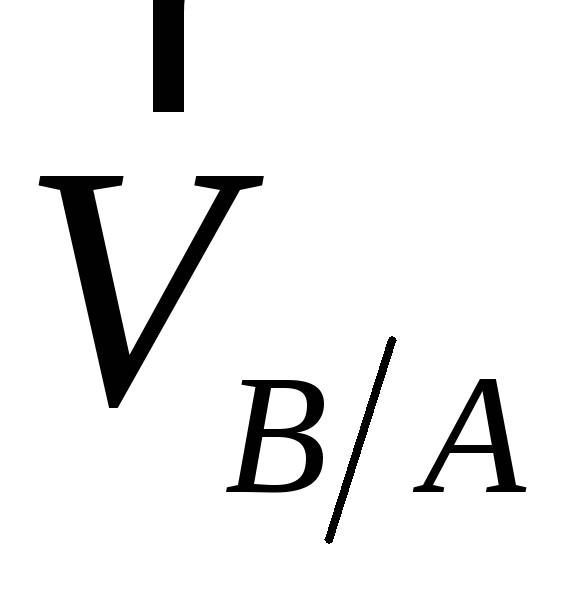 представляет собой скорость, полученную
точкой
представляет собой скорость, полученную
точкой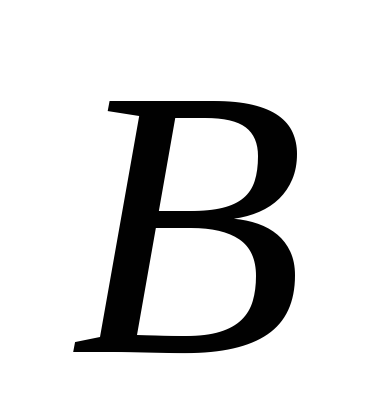
 перпендикулярно плоской фигуре. Этот
вектор направлен перпендикулярно
отрезку
перпендикулярно плоской фигуре. Этот
вектор направлен перпендикулярно
отрезку (по касательной к окружности, которую
описывает точка
(по касательной к окружности, которую
описывает точка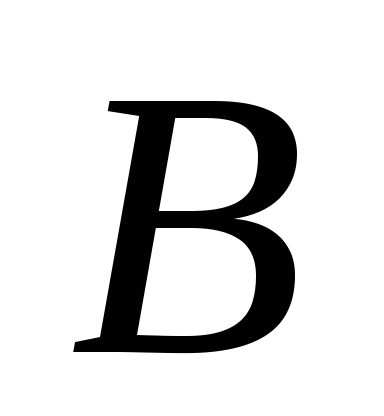 при вращении тела вокруг оси
при вращении тела вокруг оси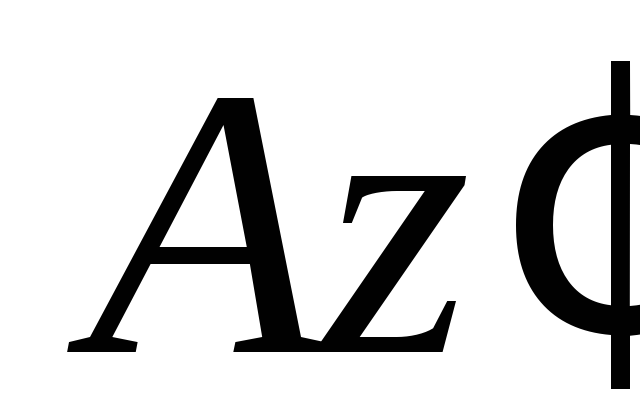 ),
причем в сторону вращения тела (Рис.
2.3). В соответствии с формулой Эйлера
),
причем в сторону вращения тела (Рис.
2.3). В соответствии с формулой Эйлера 
Пример 2.4
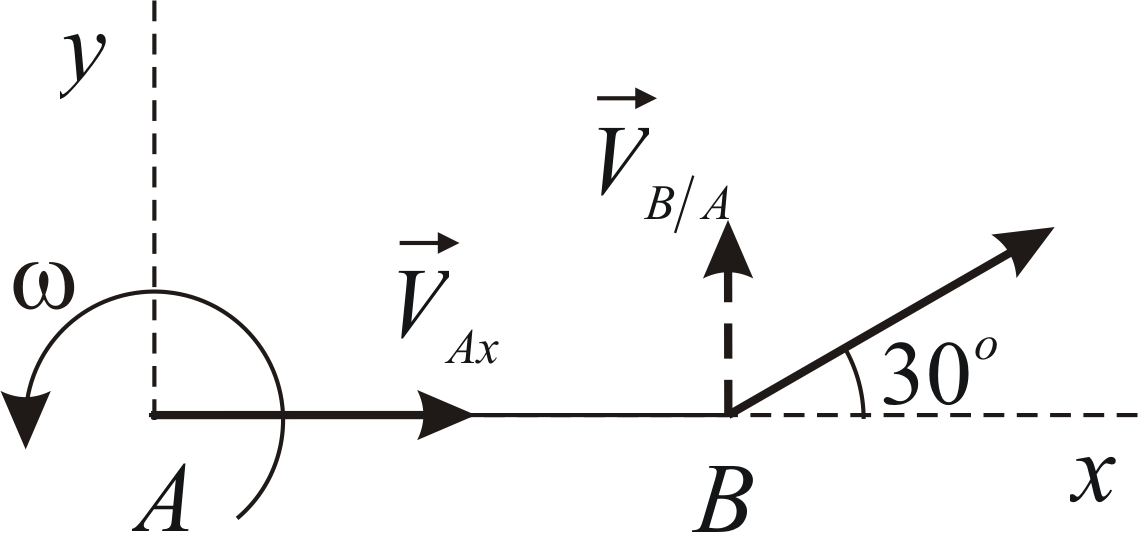
Пластина совершает плоскопараллельное
движение. В данный момент времени угловая
скорость пластины равна 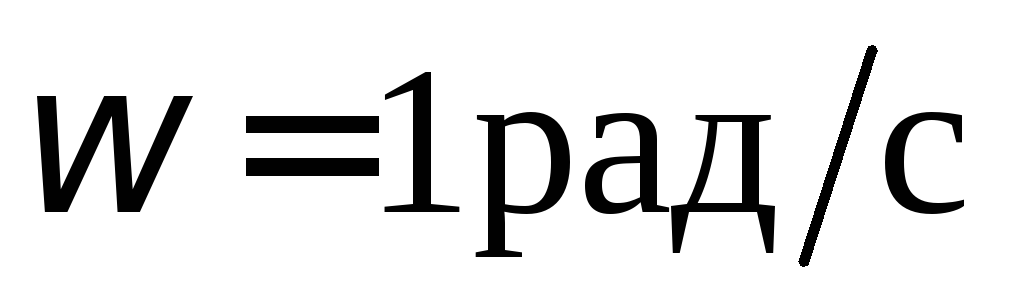 ,
проекция на ось
,
проекция на ось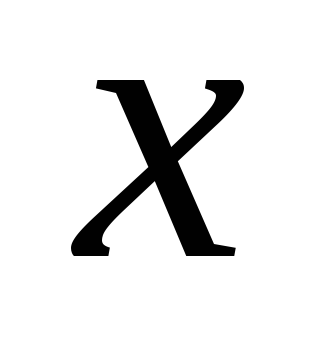 скорости точки
скорости точки пластины равна
пластины равна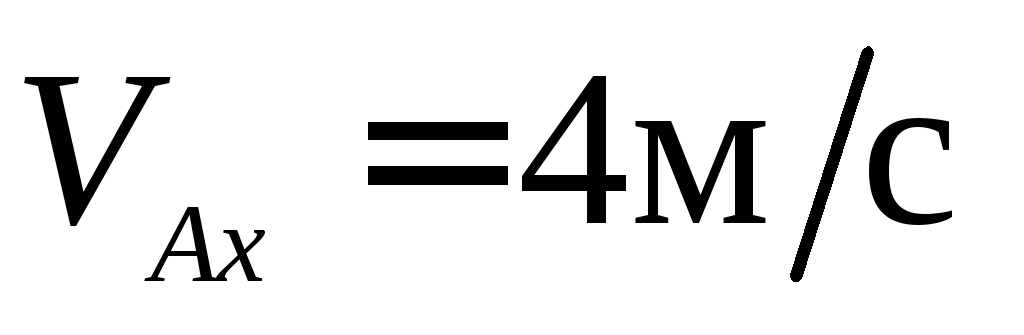
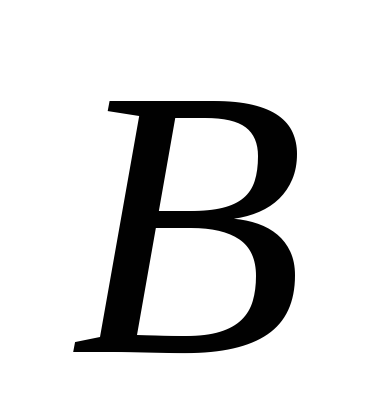 образует с осью
образует с осью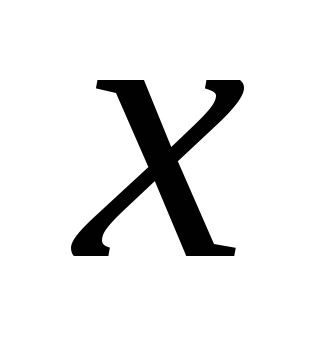 угол
угол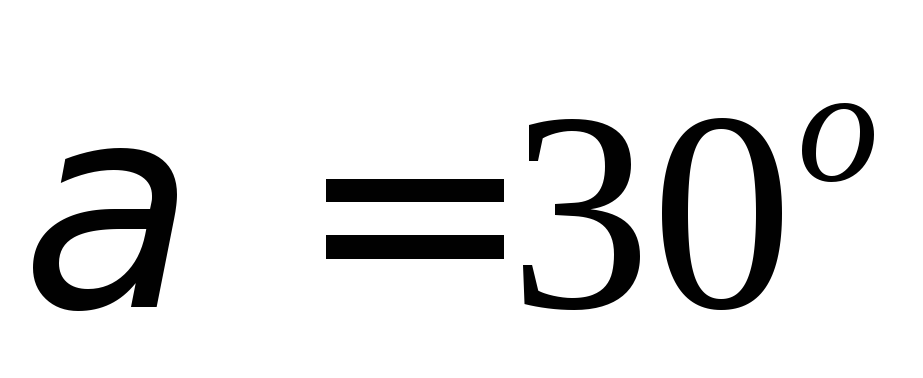 (Рис. 2.4). Определить модули скоростей
точек
(Рис. 2.4). Определить модули скоростей
точек и
и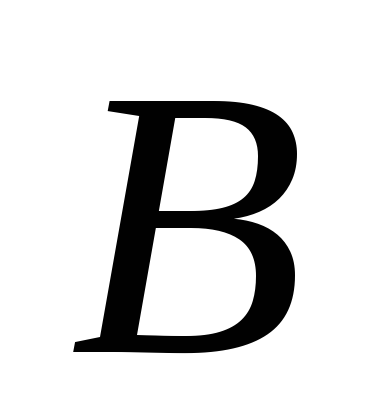 ,
если
,
если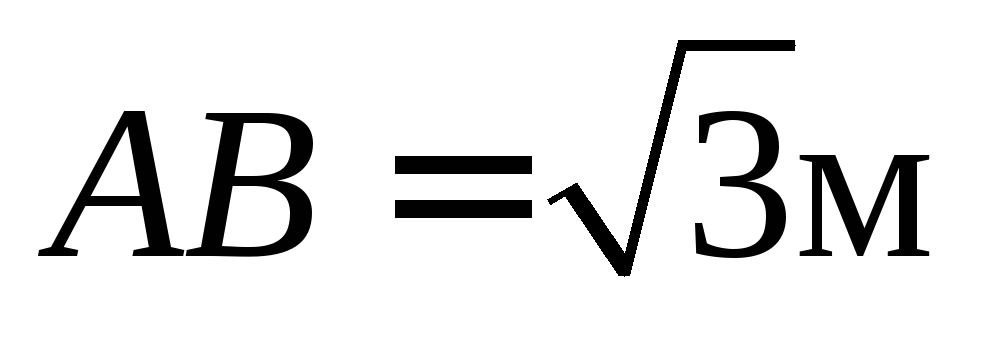
|
Рис. 2.4 |
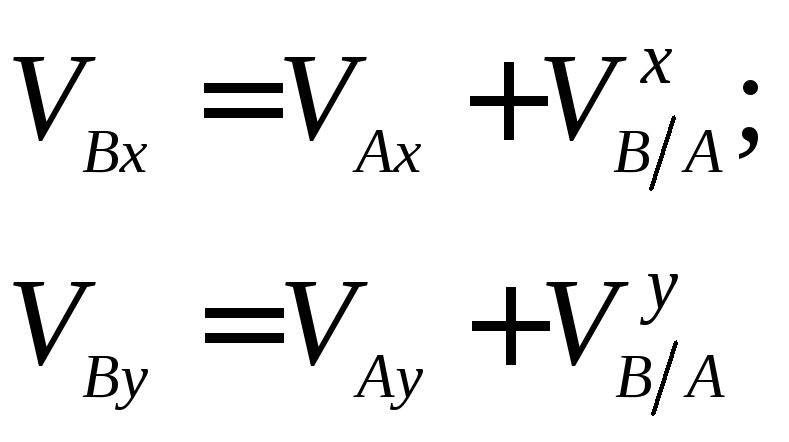 или
или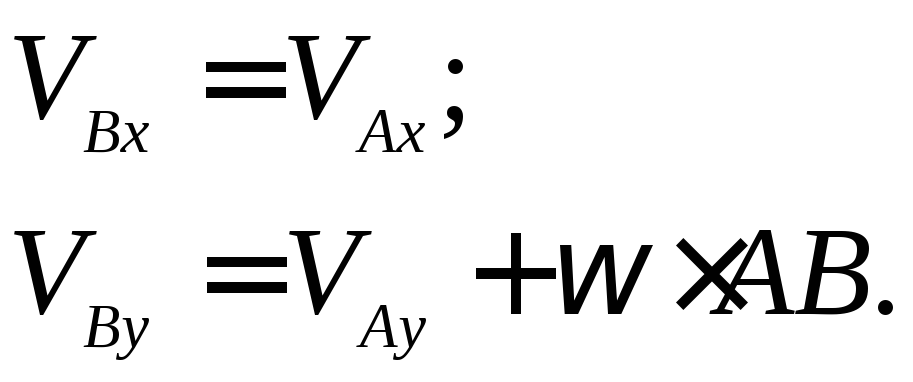
Учитывая данные задачи, получаем:
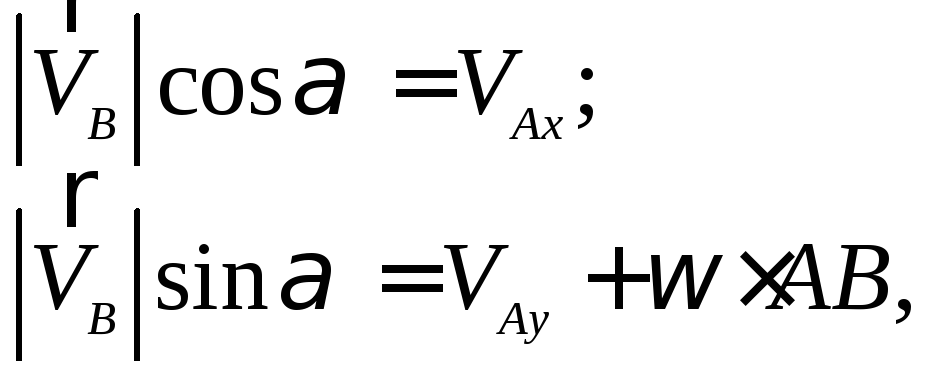
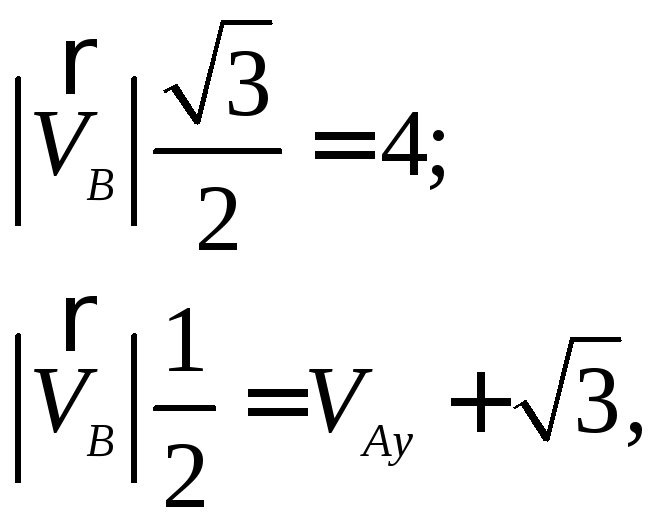
Отсюда:
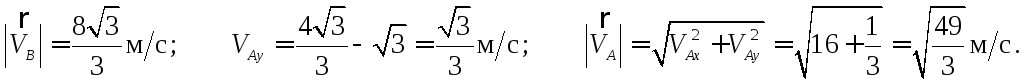
Следует заметить, что прямое
использование формулы (a)
целесообразно в довольно небольшом
числе случаев. В некоторых задачах имеет
смысл использовать так называемую
теорему о проекциях. Поскольку вектор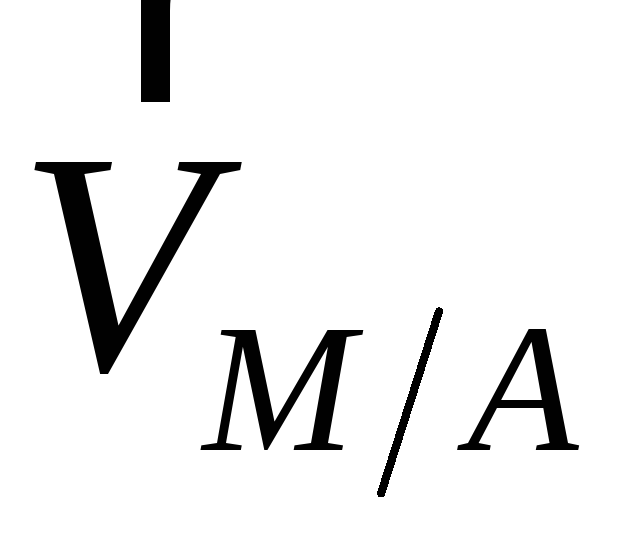 перпендикулярен отрезку
перпендикулярен отрезку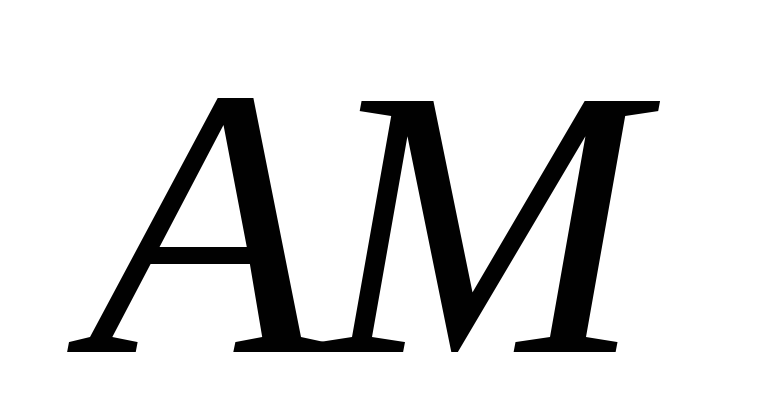
проекции скоростей концов отрезка, соединяющего две точки абсолютно твердого тела, на направление этого отрезка равны.
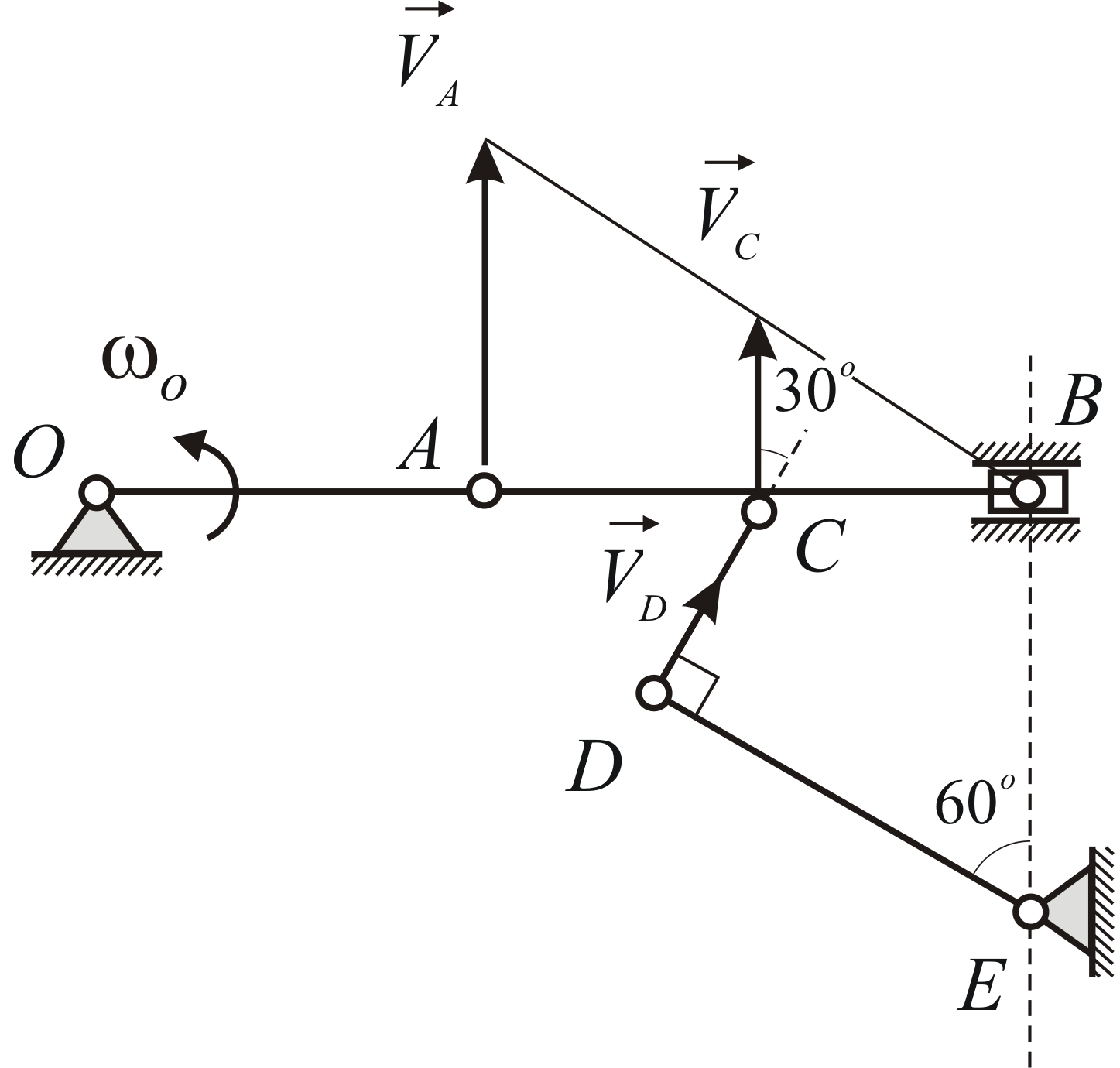
Пример 2.5
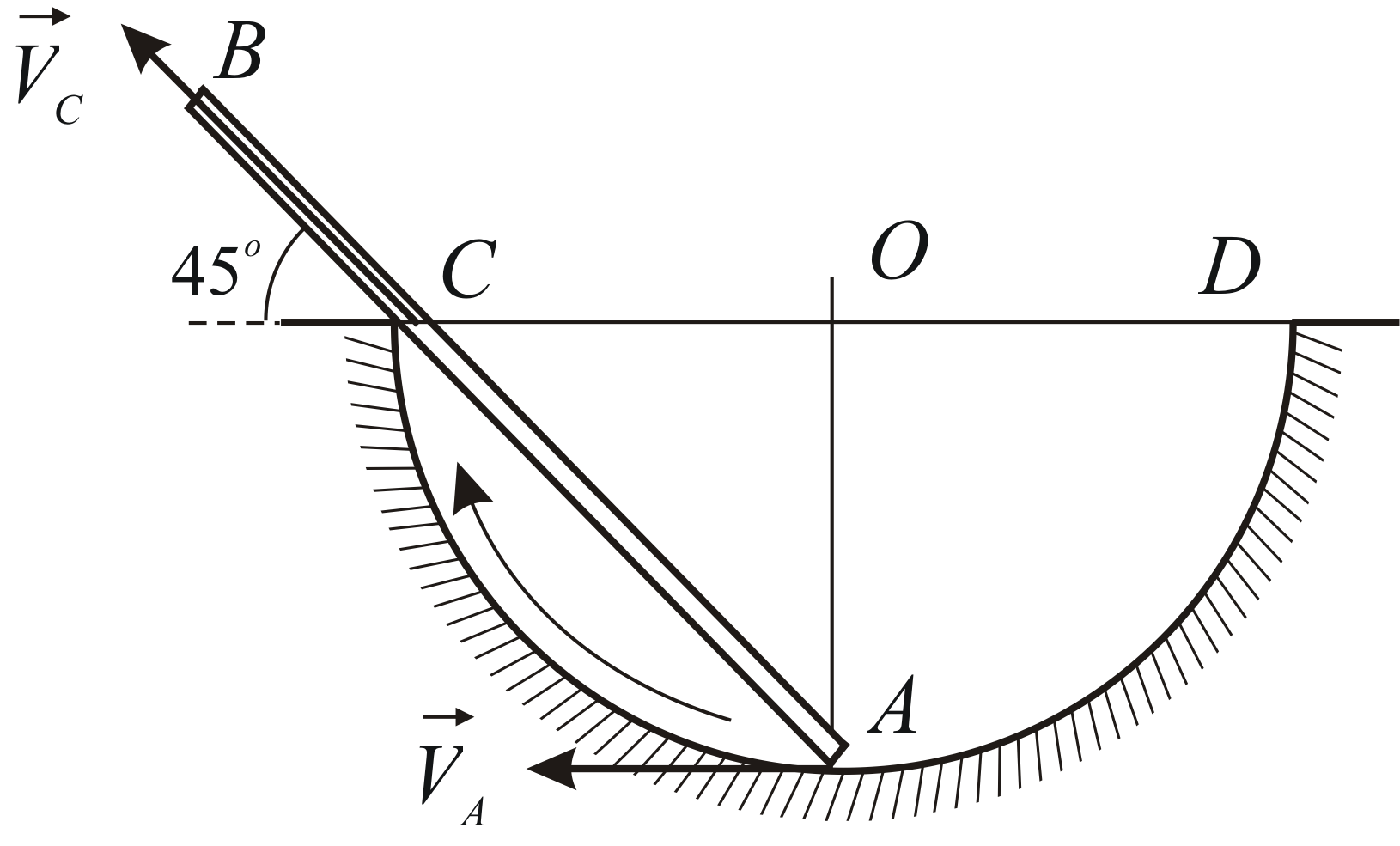
Стержень 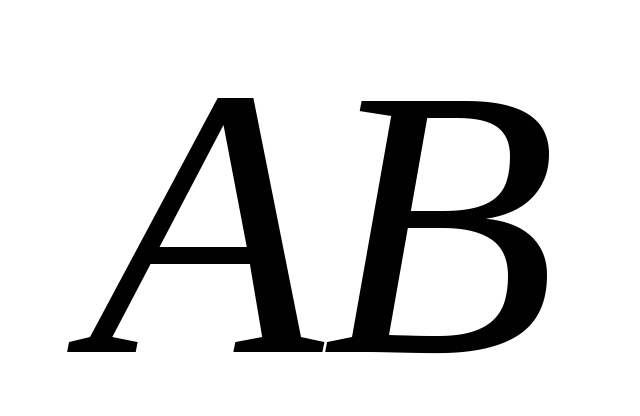 движется в плоскости рисунка, причём
его конец
движется в плоскости рисунка, причём
его конец всё время находится на полуокружности
всё время находится на полуокружности ,
а сам стержень всё время касается
неподвижного выступа
,
а сам стержень всё время касается
неподвижного выступа
 (Рис. 2.5). Определить скорость
(Рис. 2.5). Определить скорость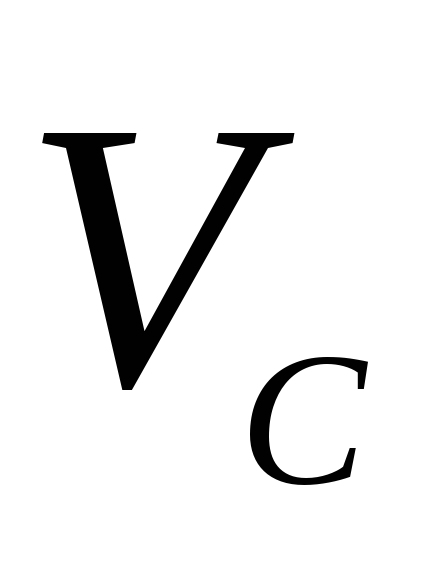 точки стержня, касающейся выступа, в
тот момент времени, когда радиус
точки стержня, касающейся выступа, в
тот момент времени, когда радиус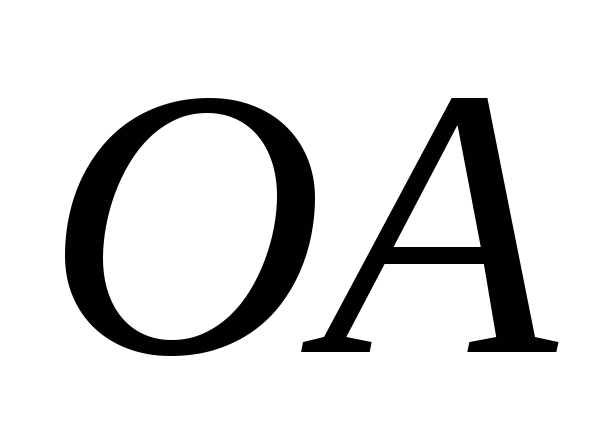 перпендикулярен
перпендикулярен ,
если известно, что скорость точки
,
если известно, что скорость точки в этот момент
в этот момент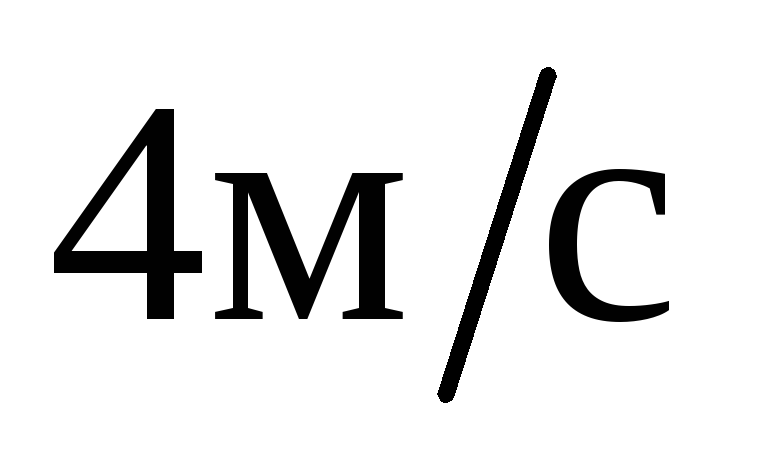
|
Рис. 2.5 |
 и
и в данный момент времени известны.
Скорость точки
в данный момент времени известны.
Скорость точки
 направлена вдоль стержня, т.к. по условию
задачи стержень не отрывается от выступа.
Таким образом, для заданного положения
стержня известны углы, которые образуют
векторы скоростей точек
направлена вдоль стержня, т.к. по условию
задачи стержень не отрывается от выступа.
Таким образом, для заданного положения
стержня известны углы, которые образуют
векторы скоростей точек и
и с отрезком
с отрезком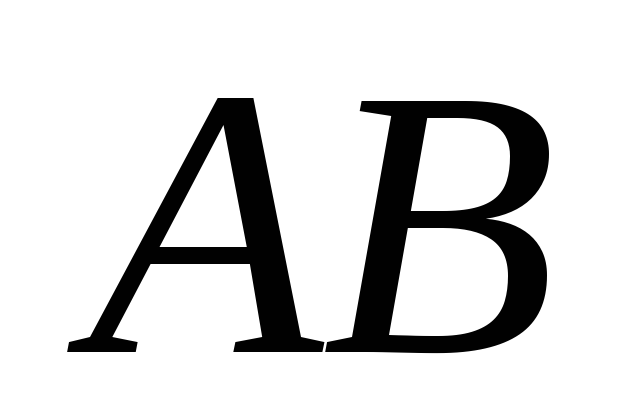
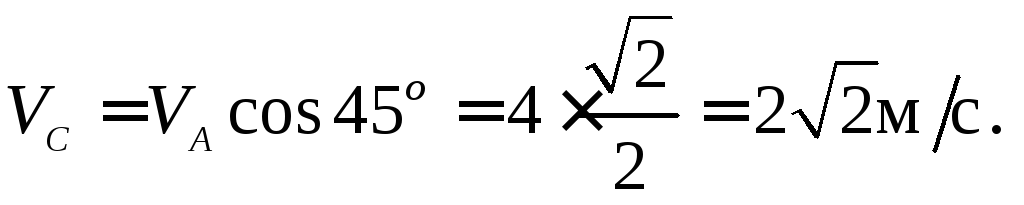
Решение задач с помощью мгновенного центра скоростей. Основной способ определения поля скоростей при плоскопараллельном движении твёрдого тела основан на использовании мгновенного центра скоростей.
Как уже говорилось, за полюс можно принять любую точку плоской фигуры. В данный момент времени различные точки тела имеют разные скорости. За полюс имеет смысл принимать точку, скорость которой в данный момент времени равна нулю.
Точка, принадлежащая плоской фигуре или неизменно с ней связанная, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей.
|
Рис. 2.6 |
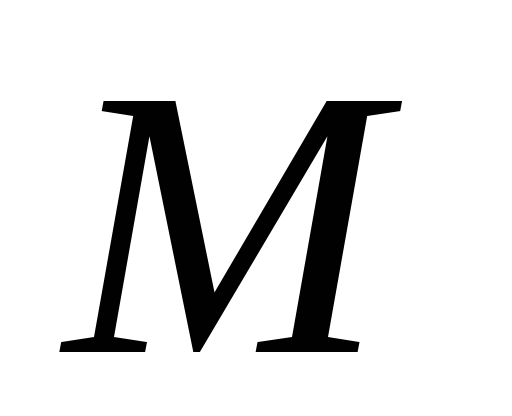 плоской фигуры определяется так же, как
если бы тело вращалось вокруг оси,
проходящей через мгновенный центр
скоростей перпендикулярно плоскости
движения плоской фигуры (Рис. 2.6):
плоской фигуры определяется так же, как
если бы тело вращалось вокруг оси,
проходящей через мгновенный центр
скоростей перпендикулярно плоскости
движения плоской фигуры (Рис. 2.6):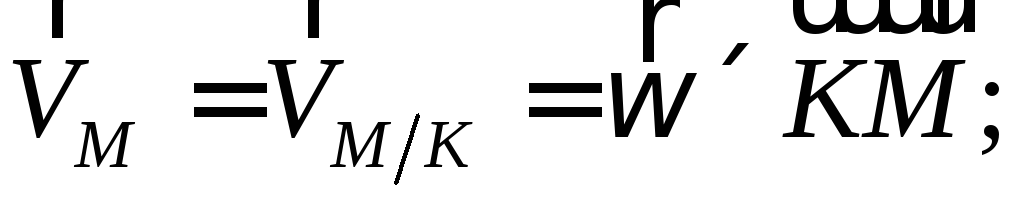
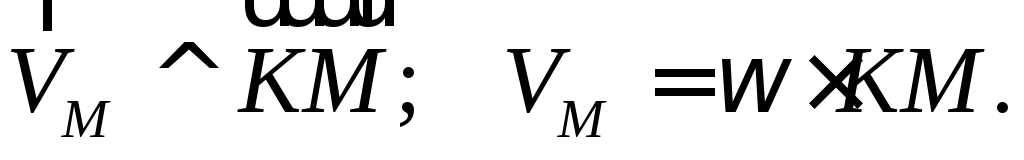
Пример 2.6
Кривошипн0-шатунный механизм связан
шарнирно в середине
шатуна со стержнем ,
а последний – со стержнем
,
а последний – со стержнем ,
который может вращаться вокруг оси
,
который может вращаться вокруг оси
 в указанном на Рис. 2.7 положении механизма,
если точки
в указанном на Рис. 2.7 положении механизма,
если точки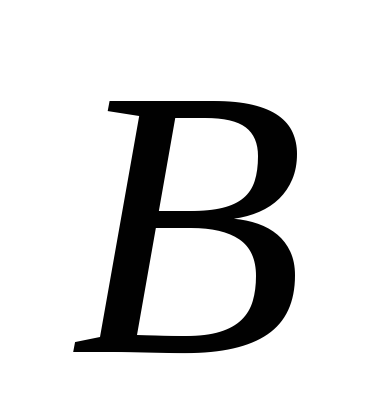 и
и расположены на одной вертикали; угловая
скорость
расположены на одной вертикали; угловая
скорость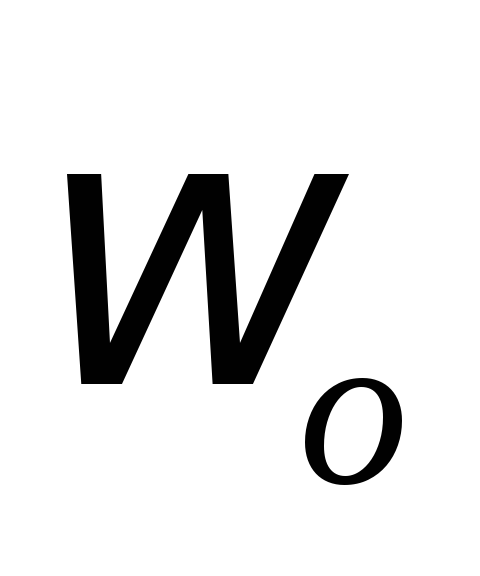 кривошипа
кривошипа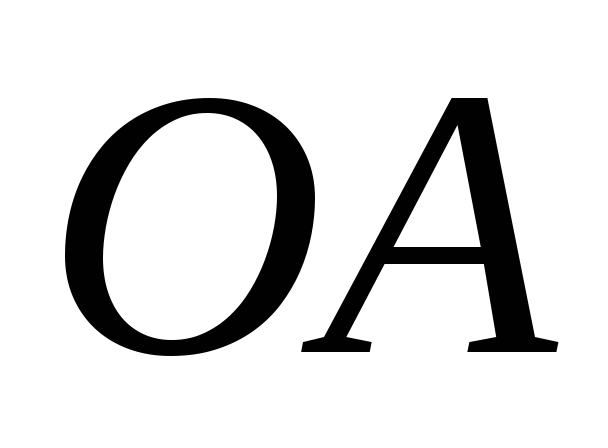 равна 8 рад/с,
равна 8 рад/с,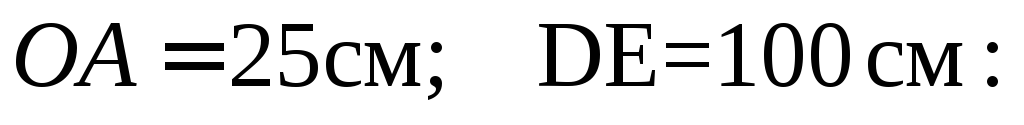
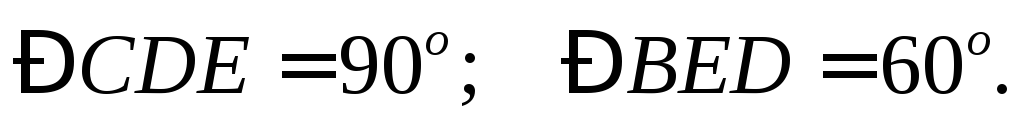
|
Рис. 2.7 |
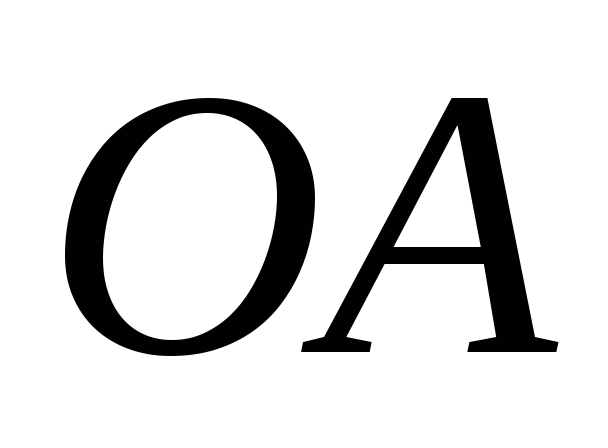 вращается вокруг неподвижной оси.
Скорость точки
вращается вокруг неподвижной оси.
Скорость точки определяем по формуле Эйлера:
определяем по формуле Эйлера: 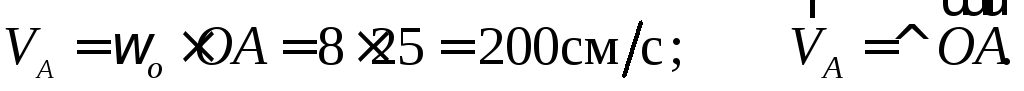
Движение стержня 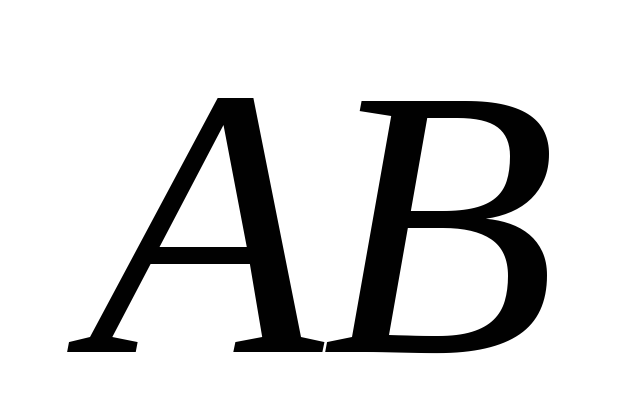 плоскопараллельное. Мгновенный центр
скоростей находится в точке
плоскопараллельное. Мгновенный центр
скоростей находится в точке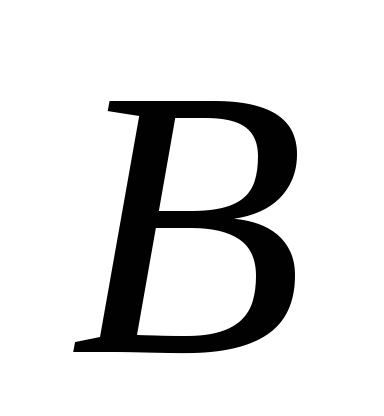 .
Учитывая, что скорости точек тела
пропорциональны расстояниям до
мгновенного центра скоростей, получаем:
.
Учитывая, что скорости точек тела
пропорциональны расстояниям до
мгновенного центра скоростей, получаем:
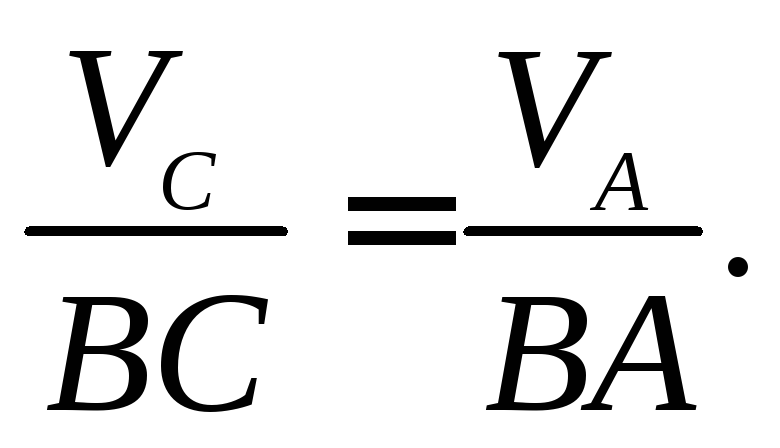 Отсюда:
Отсюда: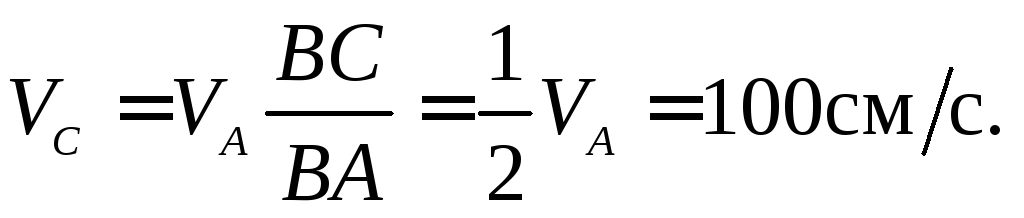
Движение стержня 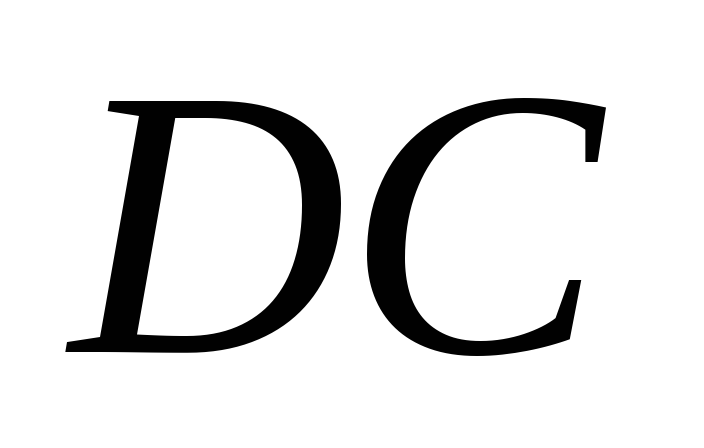 плоскопараллельное. Скорость точки
плоскопараллельное. Скорость точки направлена по касательной к окружности
радиуса
направлена по касательной к окружности
радиуса ,
которая является траекторией точки
,
которая является траекторией точки .
При заданном положении механизма
направление скорости точки
.
При заданном положении механизма
направление скорости точки совпадает с направлением стержня
совпадает с направлением стержня .
Для определения скорости точки
.
Для определения скорости точки имеет смысл использовать теорему о
проекциях скоростей:
имеет смысл использовать теорему о
проекциях скоростей:
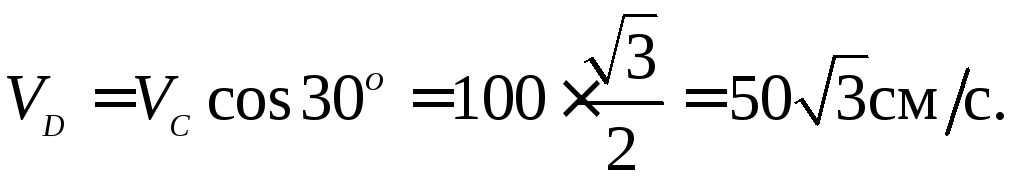
Остаётся определить угловую скорость
стержня  .
Поскольку движение этого стержня
вращательное, используем формулу Эйлера:
.
Поскольку движение этого стержня
вращательное, используем формулу Эйлера:
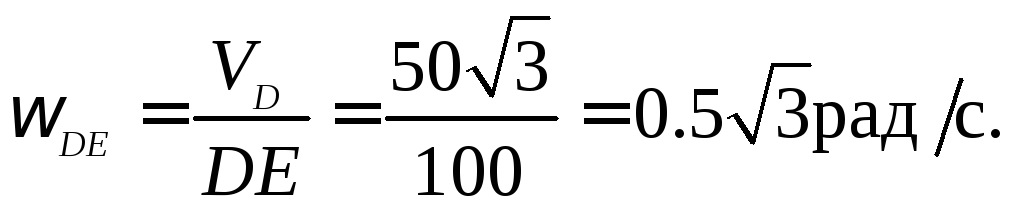
Пример 2.7
Колесо радиуса 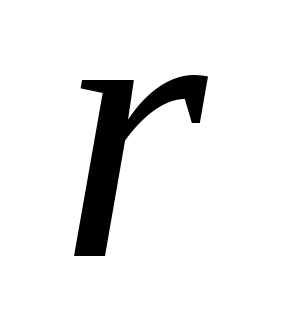 катится без скольжения по неподвижной
поверхности (Рис. 2.8). Скорость центра
колеса
катится без скольжения по неподвижной
поверхности (Рис. 2.8). Скорость центра
колеса .
Определить скорости точек
.
Определить скорости точек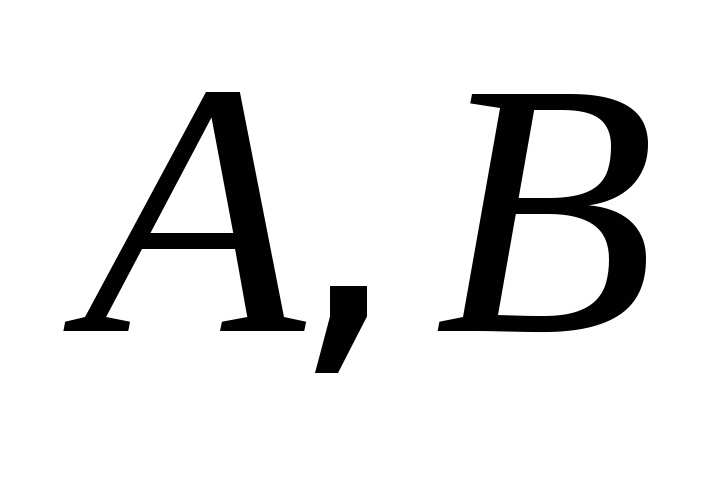 и
и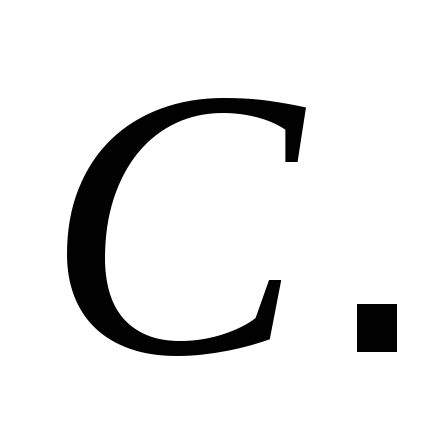
|
Рис. 2.8 |
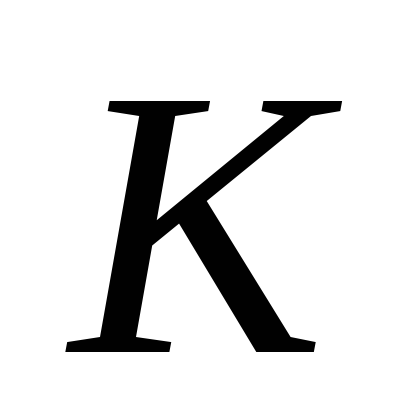 находится в точке касания колеса и
дороги. Зная скорость центра, находим
угловую скорость колеса:
находится в точке касания колеса и
дороги. Зная скорость центра, находим
угловую скорость колеса: 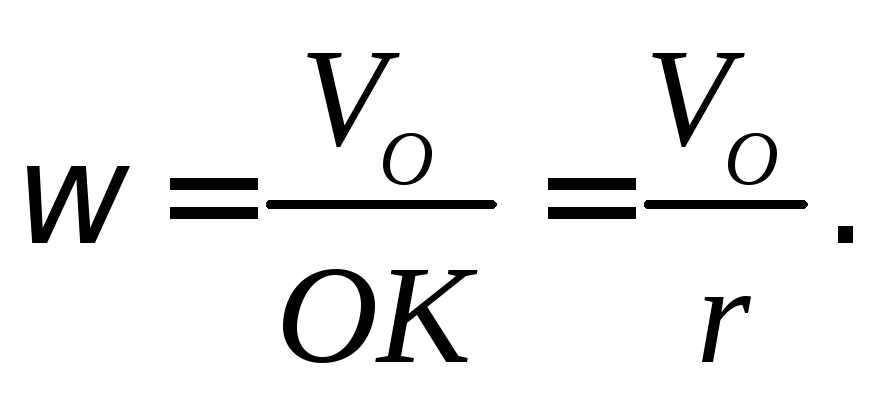
Скорости точек колеса определяем по формуле Эйлера:
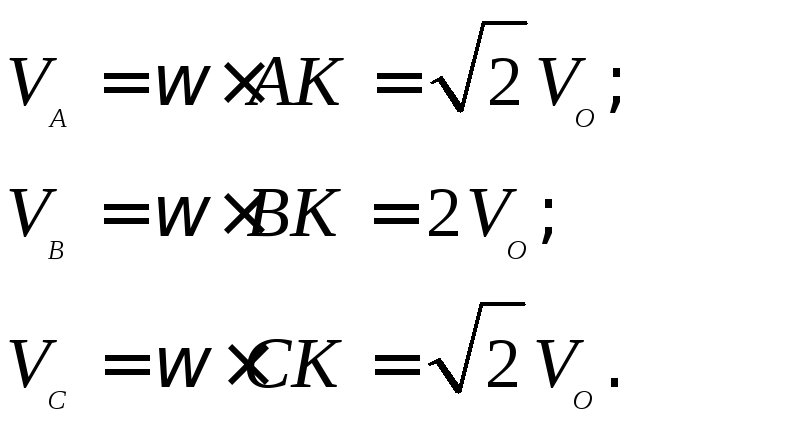

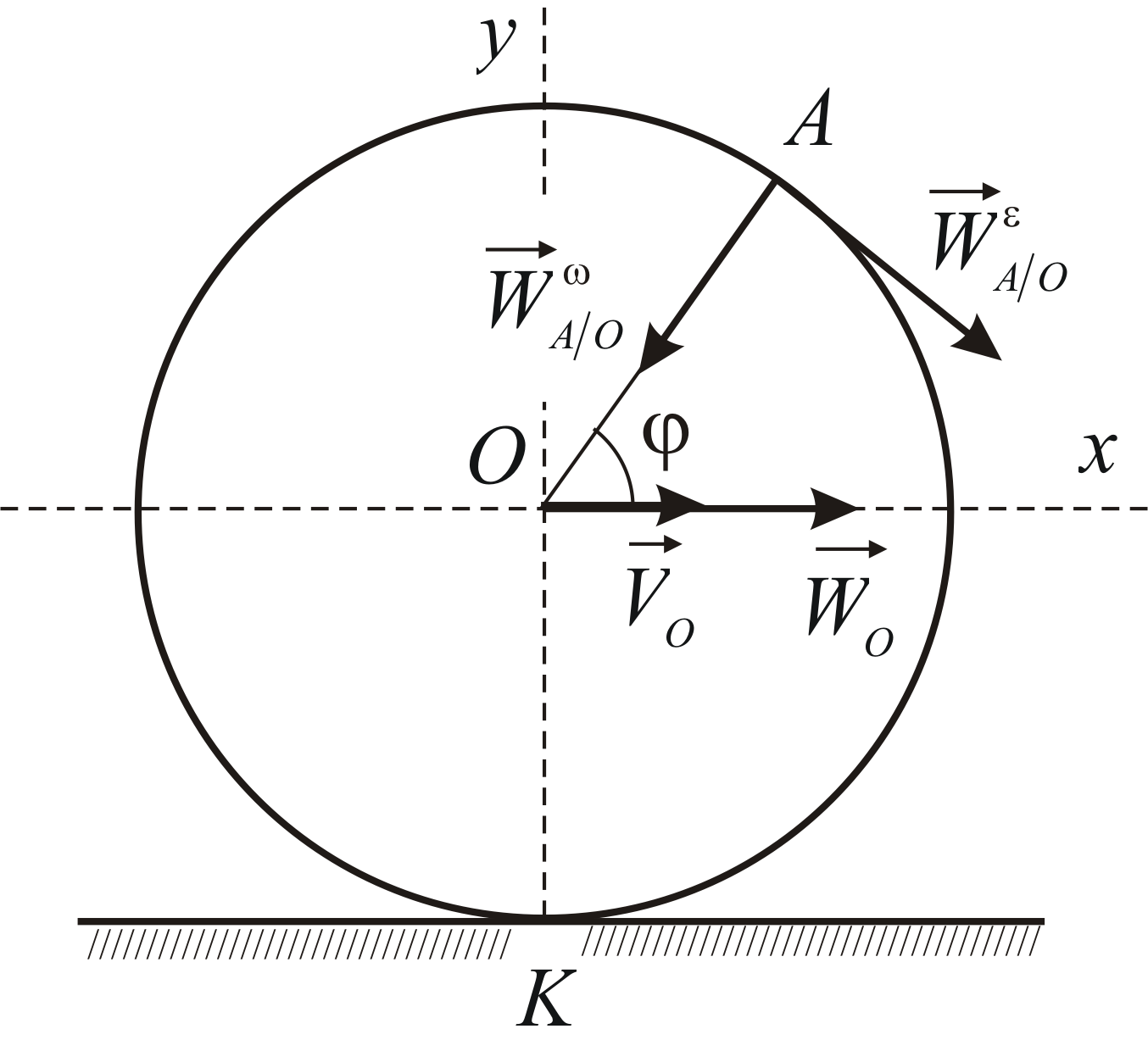
Качение колеса представляет интерес еще и в том отношении, что позволяет проиллюстрировать смысл формулы (a). Пусть колесо, движение которого мы рассматриваем, – ведущее колесо, т.е. оно принудительно вращается некоторым приводом. Рассмотрим возможные режимы движения.
Может случиться так, что колесо
вращается, но автомобиль не перемещается
– буксует. В этом случае движение колеса
представляет собой вращение вокруг
неподвижной оси  .
Все точки колеса будут описывать
окружности с центром в точке
.
Все точки колеса будут описывать
окружности с центром в точке ,
радиусы которых равны расстояниям от
этих точек до оси колеса. Скорость любой
точки направлена по касательной к этой
окружности и определяется по формуле
Эйлера.
,
радиусы которых равны расстояниям от
этих точек до оси колеса. Скорость любой
точки направлена по касательной к этой
окружности и определяется по формуле
Эйлера.
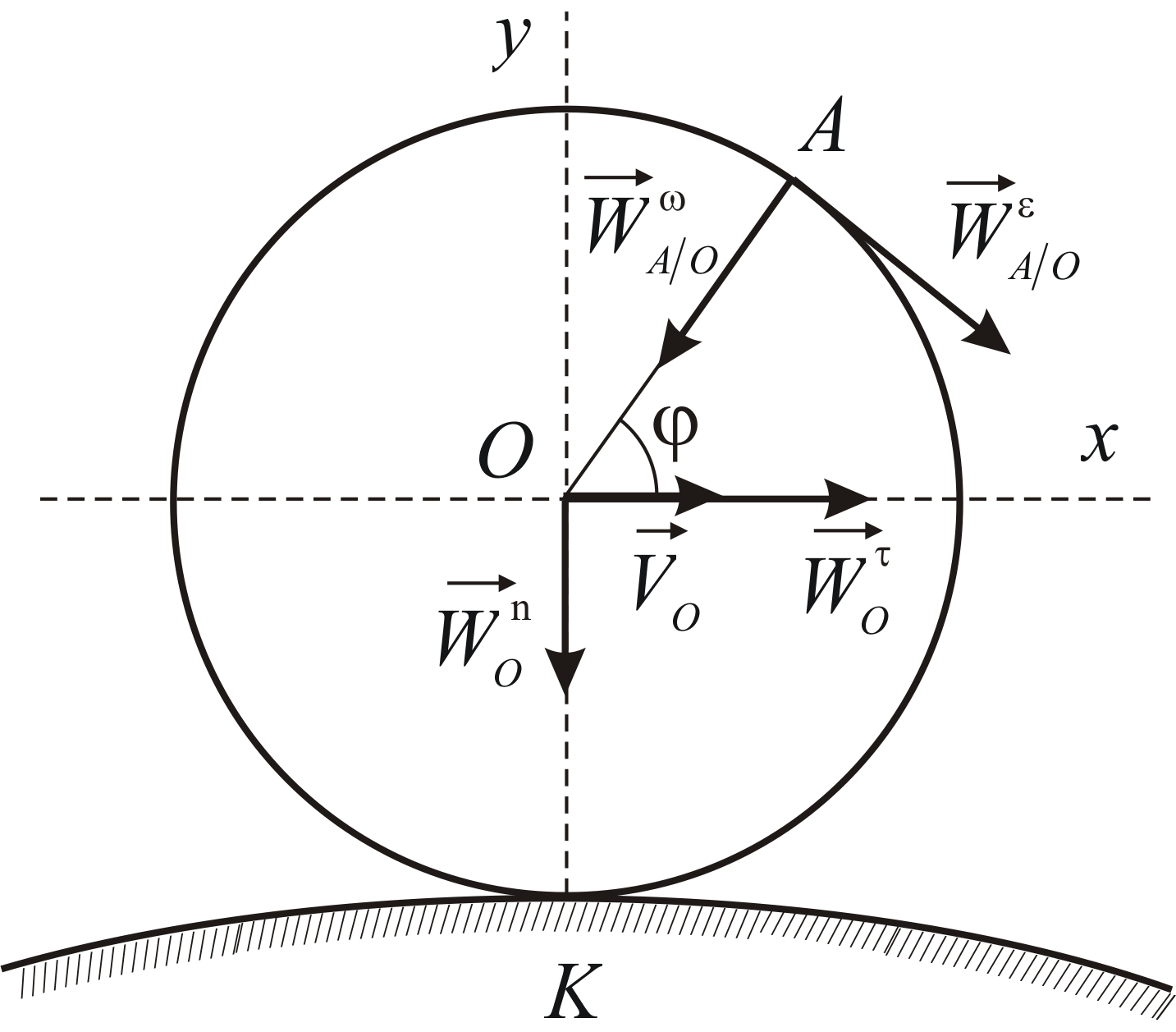
Другое возможное движение колеса
представляет собой качение с
проскальзыванием. Автомобиль при этом
перемещается, но колеса вращаются
несоразмерно быстро. Скорость оси колеса
отлична от нуля и вступает в свои права
формула (a). Скорость,
например, точки ,
которая в первом случае была ее полной
скоростью, становится скоростью,
полученной точкой
,
которая в первом случае была ее полной
скоростью, становится скоростью,
полученной точкой при вращении колеса вокруг оси
при вращении колеса вокруг оси .
Полная же скорость точки
.
Полная же скорость точки теперь геометрически складывается из
скорости точки
теперь геометрически складывается из
скорости точки и скорости, полученной точкой
и скорости, полученной точкой при вращении колеса вокруг оси
при вращении колеса вокруг оси
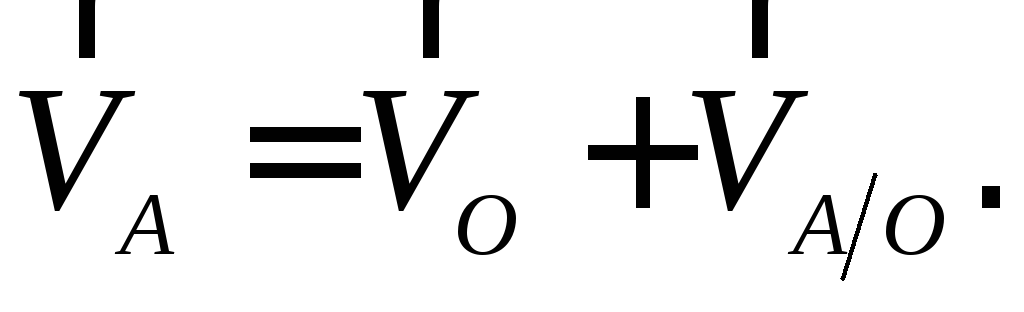
Заметим, что в этом случае движение оси (т.е. автомобиля) и вращение колеса происходят независимо друг от друга и каждое из них должно быть задано.
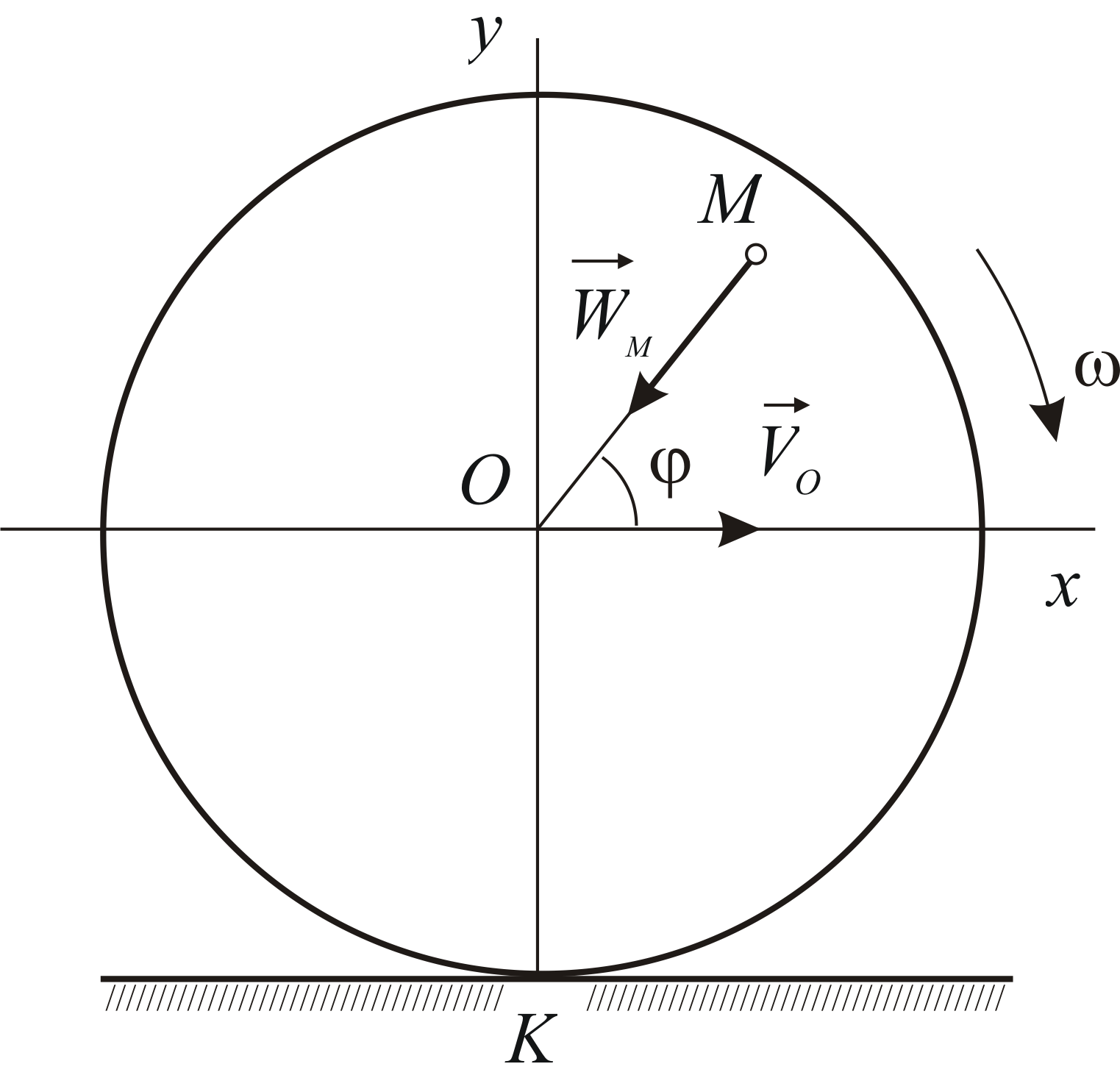
Последний режим движения колеса –
качение без скольжения. Именно этот
случай рассмотрен в примере 2.7. Движение
оси и вращение колеса оказываются
взаимосвязанными. В каждое мгновение
очевидно положение точки, скорость
которой равна нулю. В такой ситуации
при определении скоростей точек колеса
удобнее за полюс брать не точку 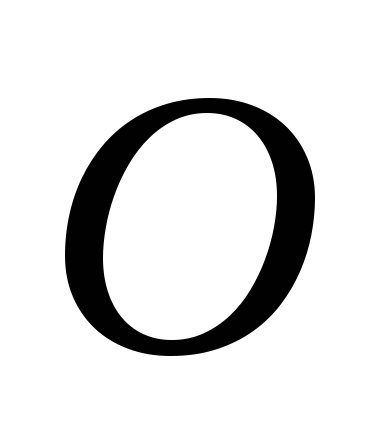 ,
а мгновенный центр скоростей
,
а мгновенный центр скоростей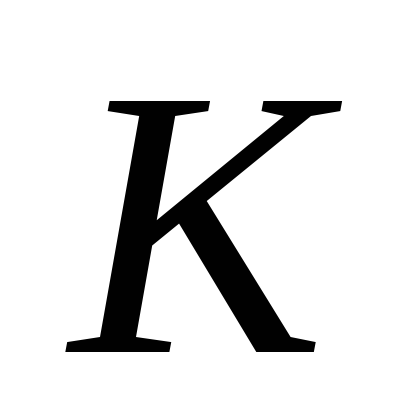 .
.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 16.3; 16.10; 16.15; 16.16; 16.19; 16.24; 16.28; 16.29; 16.31; 16.32; 16.33; 16.34; 16.35; 16.36; 16.38; 16.39.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА — теория и практика»: комплект СР-20.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6
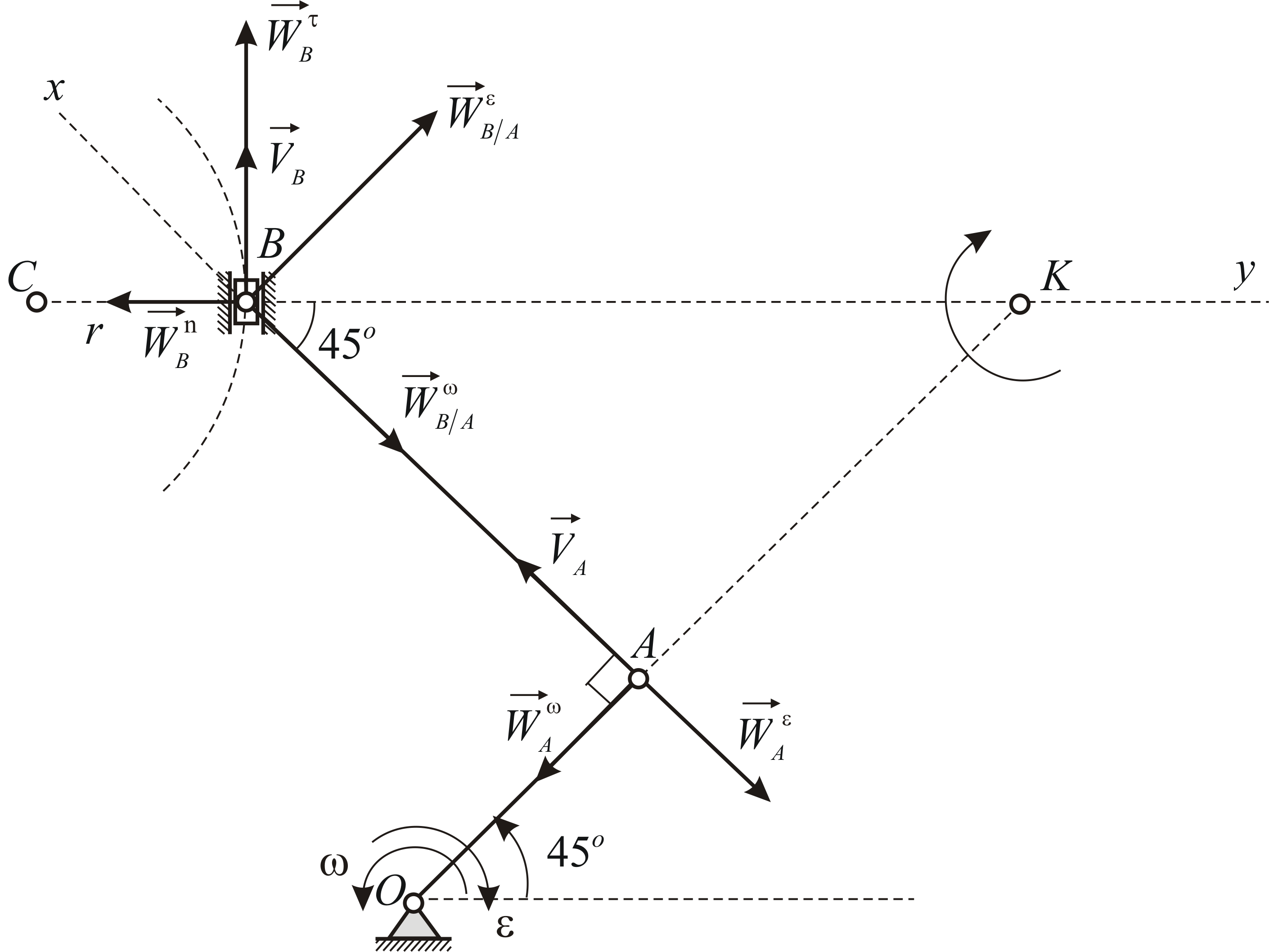
Пример 2.8
Определить скорость и ускорение ползуна 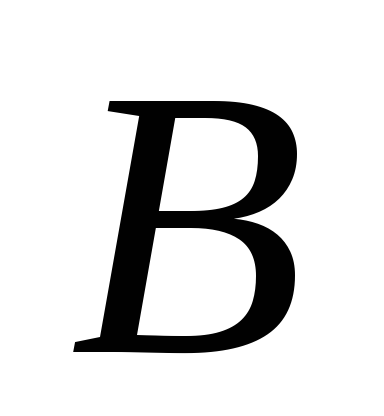 кривошипного механизма, а также угловую
скорость и угловое ускорение шатуна
кривошипного механизма, а также угловую
скорость и угловое ускорение шатуна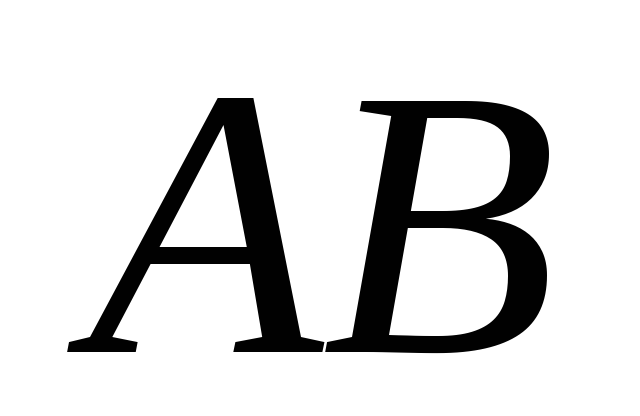 в положении, изображенном на Рис. 2.9.
Кривошип
в положении, изображенном на Рис. 2.9.
Кривошип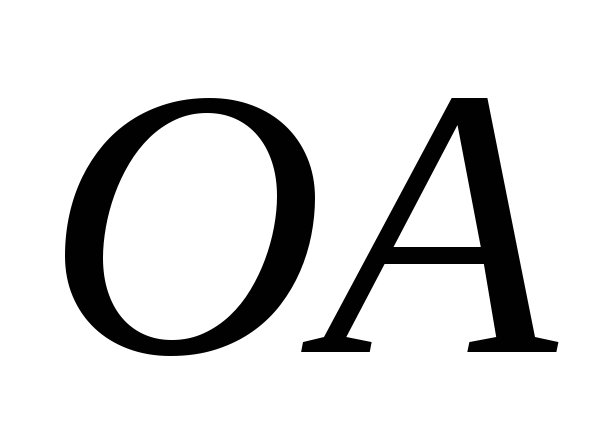 вращается замедленно, имея в данный
момент времени угловую скорость
вращается замедленно, имея в данный
момент времени угловую скорость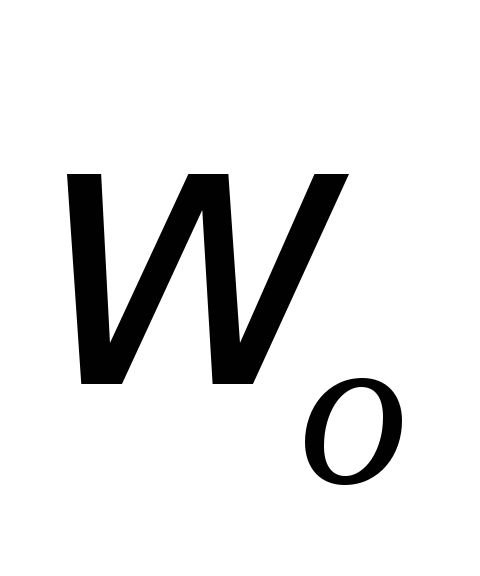 и угловое ускорение
и угловое ускорение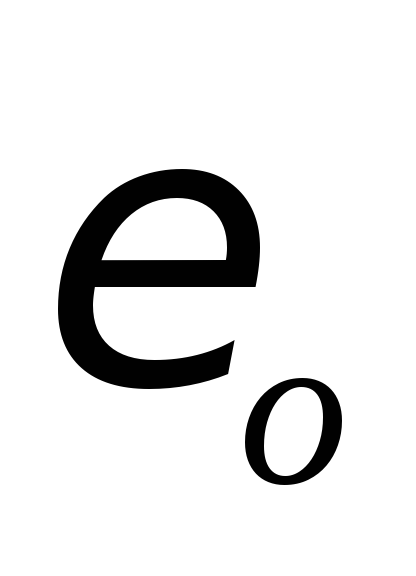 .
Ползун движется по криволинейной
направляющей, имеющей в данном положении
механизма радиус кривизны
.
Ползун движется по криволинейной
направляющей, имеющей в данном положении
механизма радиус кривизны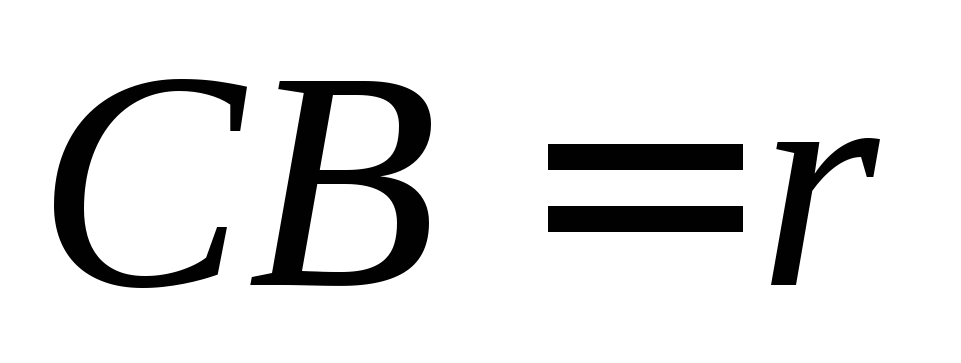 .
Дано:
.
Дано: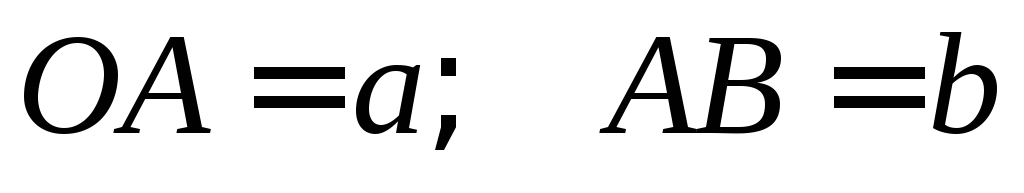 .
.
Зная направления скоростей точек  и
и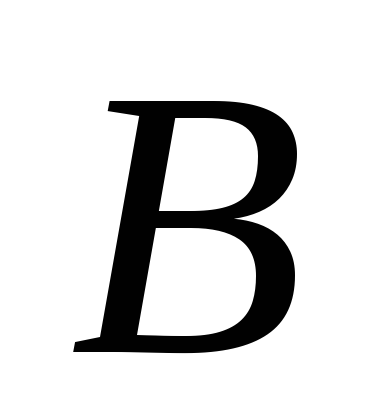 ,
построим мгновенный центр скоростей
,
построим мгновенный центр скоростей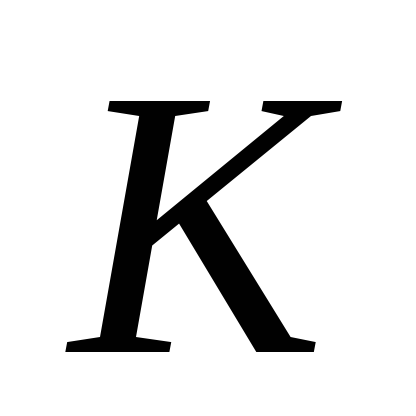 стержня
стержня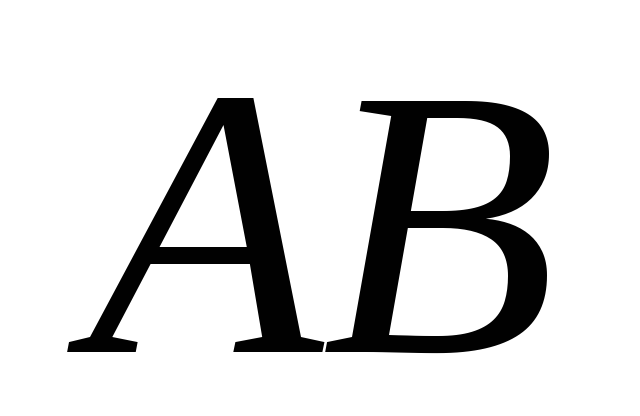 ,
после чего определим угловую скорость
стержня
,
после чего определим угловую скорость
стержня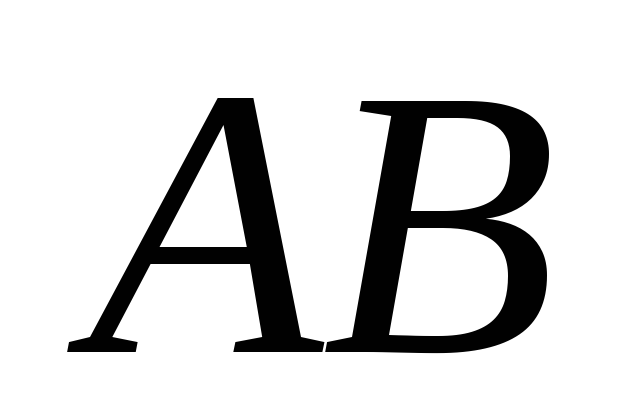
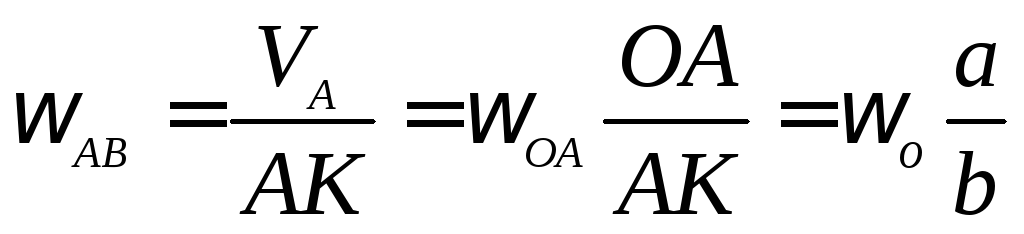
и скорость точки 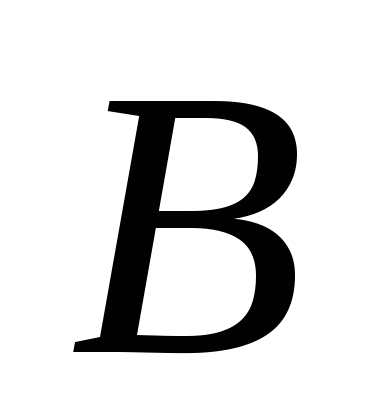

Попытка определить угловое ускорение
стержня 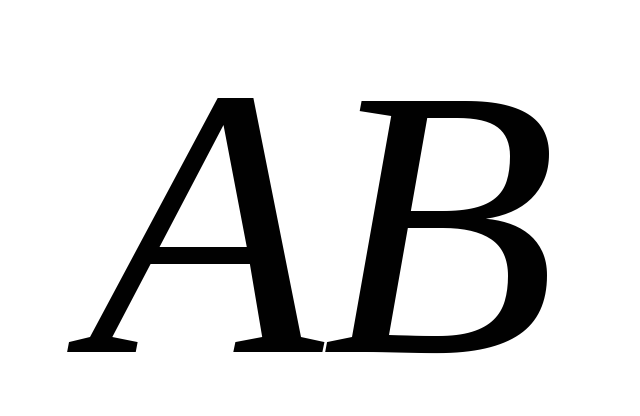 ,
используя определение
,
используя определение
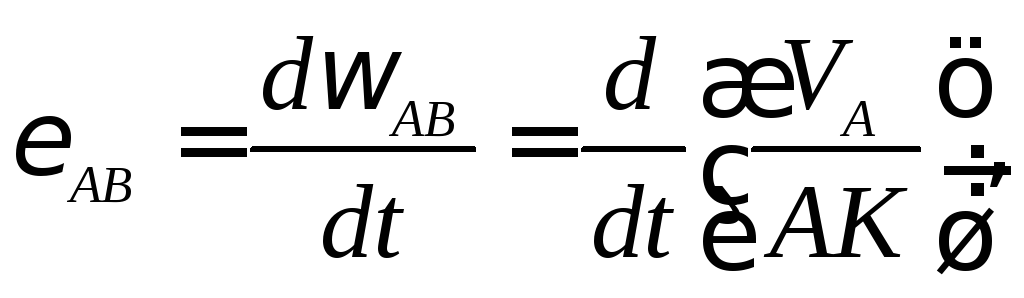
закончится неудачей, поскольку зависимость 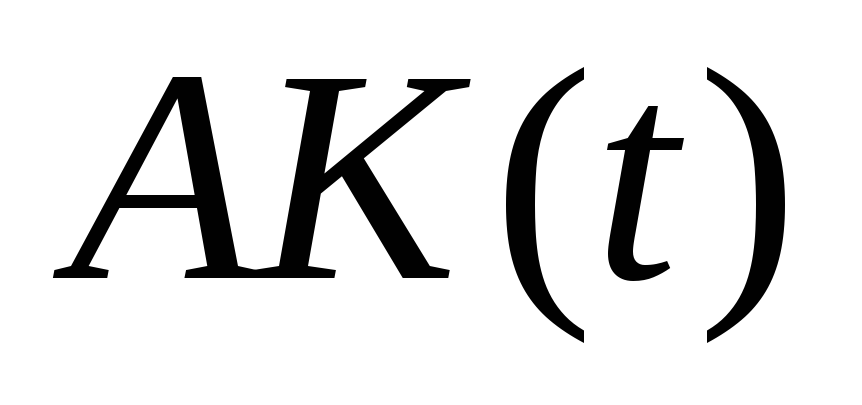 неизвестна.
неизвестна.
Для определения ускорения точки 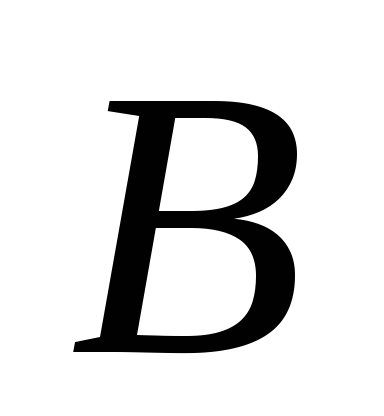 принимаем за полюс точку
принимаем за полюс точку .
Поскольку известны траектории всех
точек во всех их движениях, представим
ускорения точек их составляющими:
.
Поскольку известны траектории всех
точек во всех их движениях, представим
ускорения точек их составляющими:
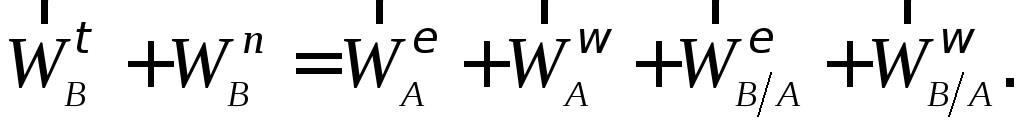
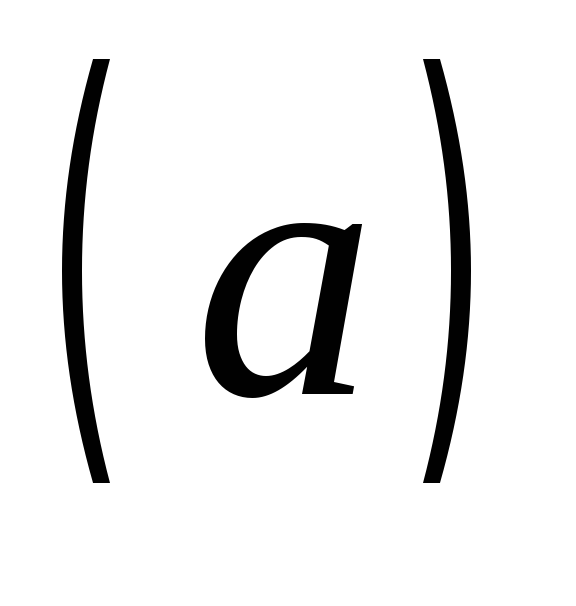
Вычислим векторы, входящие в уравнение  .
.
|
Рис. 2.9 |
Точка  принадлежит вращающемуся телу
принадлежит вращающемуся телу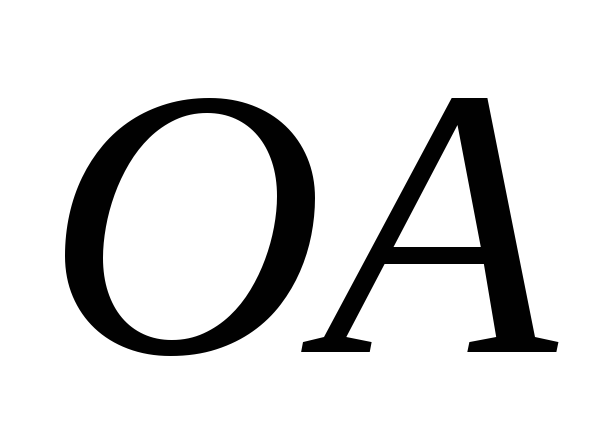 .
Определяем модули составляющих ускорения
этой точки:
.
Определяем модули составляющих ускорения
этой точки:

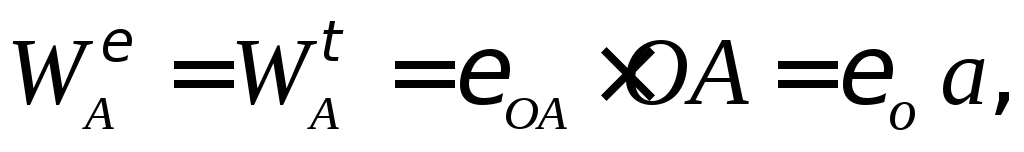
направления векторов показаны на Рис. 2.9.
Точка 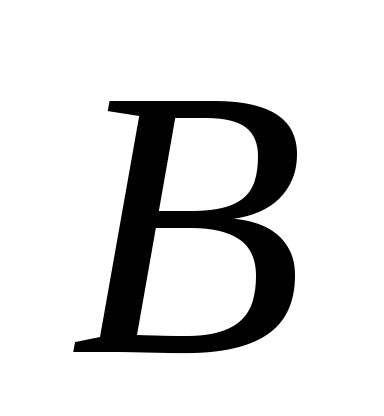 движется по криволинейной направляющей.
Касательное и нормальное ускорения
точки
движется по криволинейной направляющей.
Касательное и нормальное ускорения
точки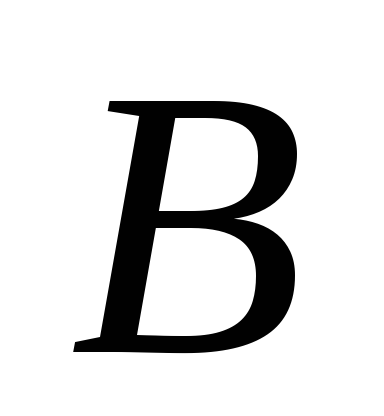 определяются по формулам:
определяются по формулам:
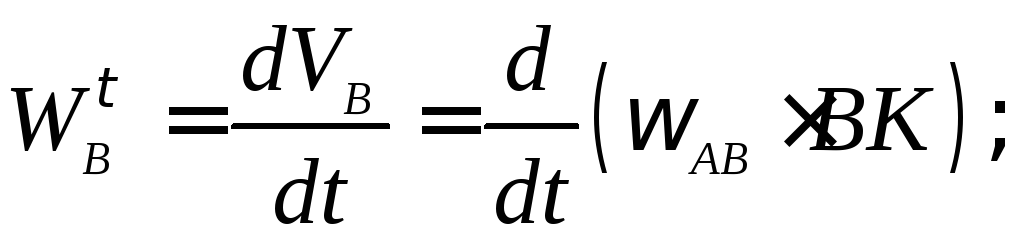
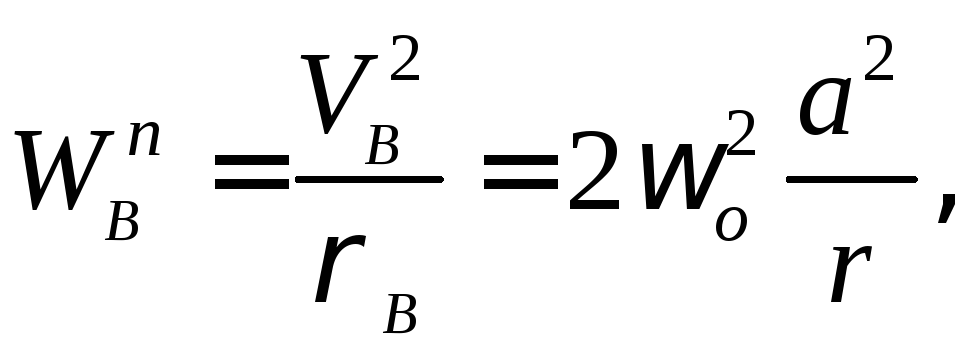
направления составляющих ускорения
показаны на Рис. 2.9. По приведенной
формуле не удается вычислить касательное
ускорение точки 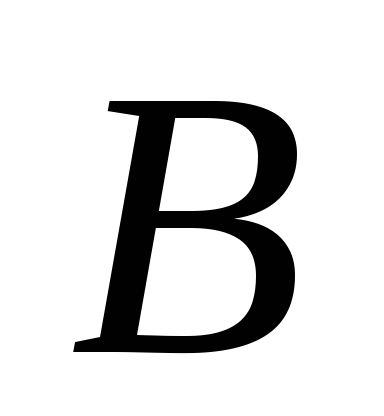 ,
поскольку неизвестны зависимости
расстояний
,
поскольку неизвестны зависимости
расстояний и
и от времени.
от времени.
Находим составляющие ускорения,
полученного точкой  при вращении шатуна
при вращении шатуна вокруг оси
вокруг оси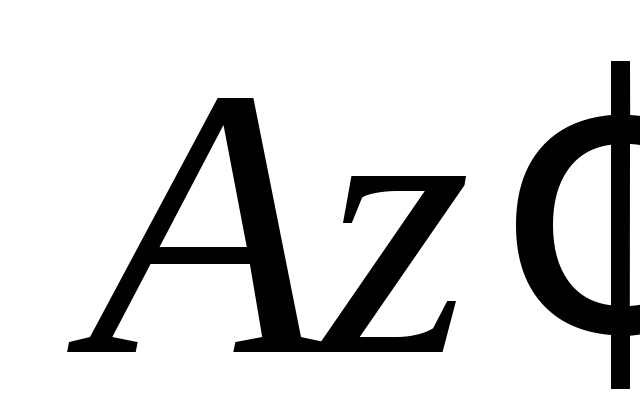 .
Заметим, что вращательное ускорение
остается неизвестным по модулю, поскольку
неизвестно угловое ускорение шатуна:
.
Заметим, что вращательное ускорение
остается неизвестным по модулю, поскольку
неизвестно угловое ускорение шатуна:
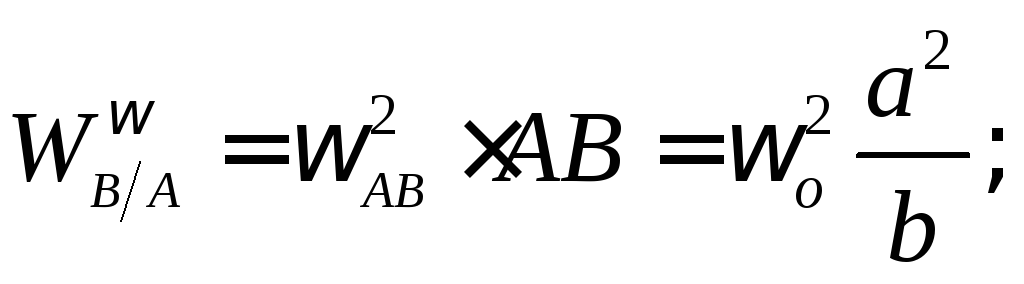
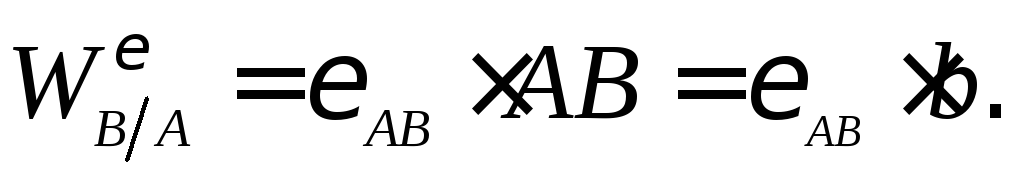
Таким образом, из шести векторов,
входящих в равенство  ,
только два неизвестны по модулю. Определим
эти неизвестные из уравнения
,
только два неизвестны по модулю. Определим
эти неизвестные из уравнения .
Это уравнение можно решить аналитически
или геометрически. Рассмотрим оба
способа решения.
.
Это уравнение можно решить аналитически
или геометрически. Рассмотрим оба
способа решения.
Имеет смысл выбрать координатные
оси так, чтобы в каждое уравнение в
проекциях входила только одна неизвестная.
Направим ось 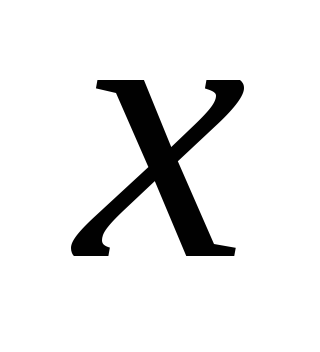 вдоль
вдоль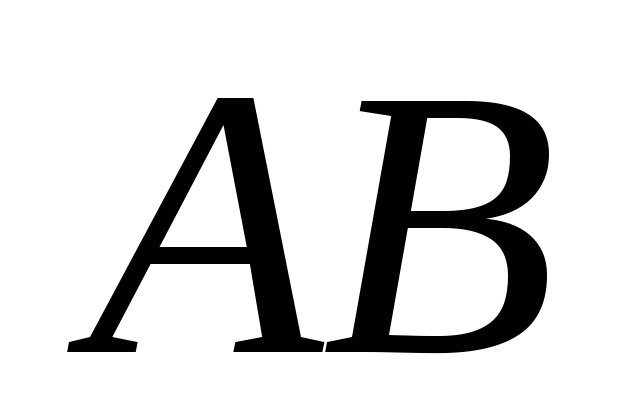 (перпендикулярно
(перпендикулярно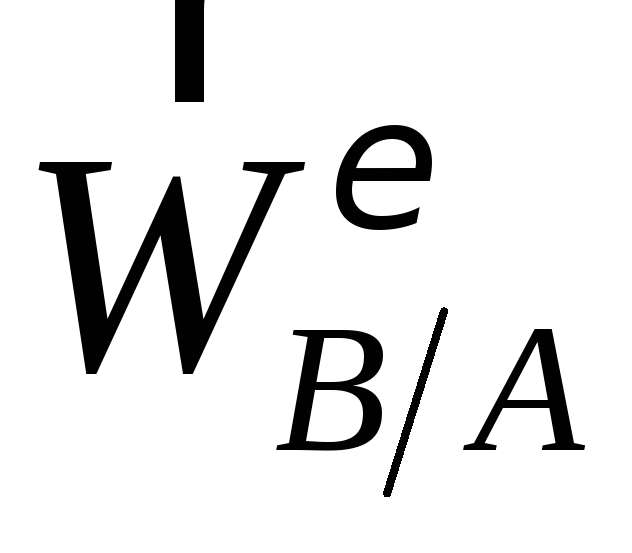 ),
а ось
),
а ось по направлению
по направлению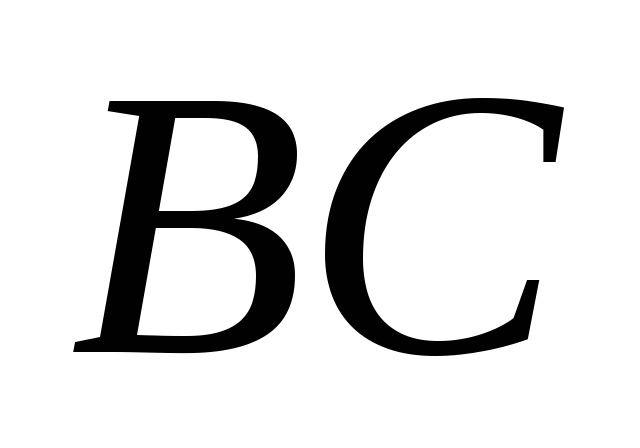 (перпендикулярно
(перпендикулярно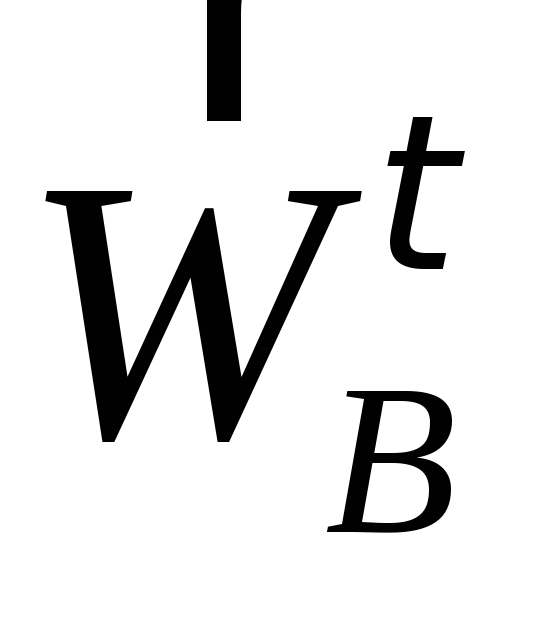 ).
Записывая уравнение
).
Записывая уравнение в проекциях на ось
в проекциях на ось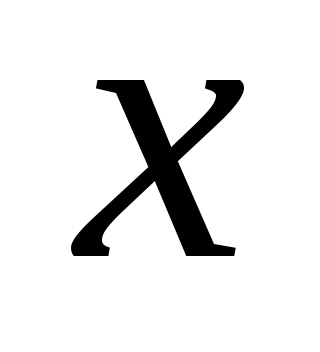 ,
получаем:
,
получаем:
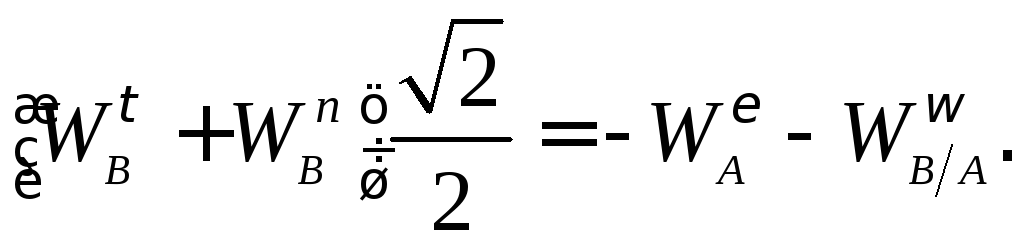
Отсюда
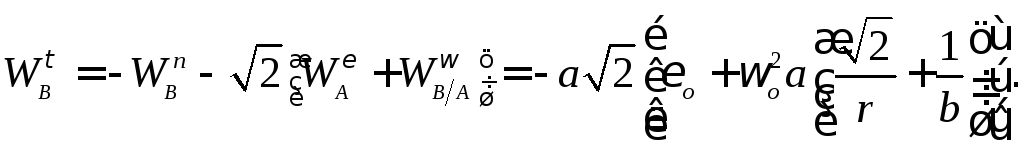
Отрицательный знак говорит о том,
что предполагаемое направление вектора 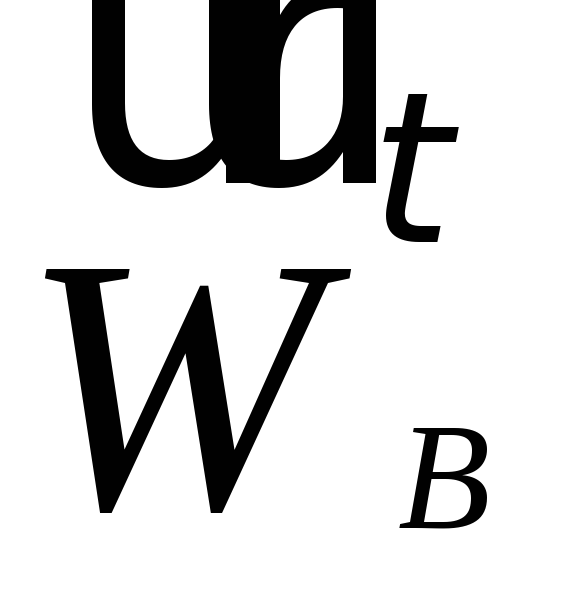 было выбрано ошибочно; в действительности
этот вектор направлен в противоположную
сторону.
было выбрано ошибочно; в действительности
этот вектор направлен в противоположную
сторону.
Записывая уравнение  в проекциях на ось
в проекциях на ось ,
получаем:
,
получаем:
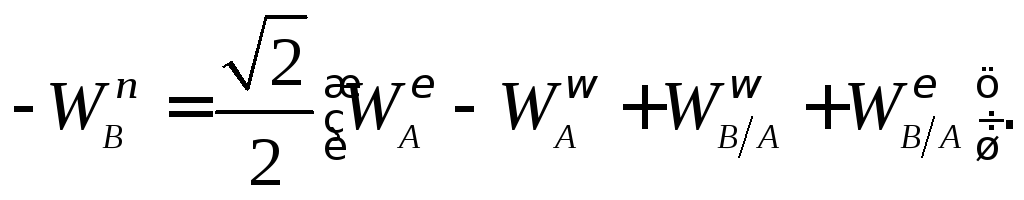
Отсюда
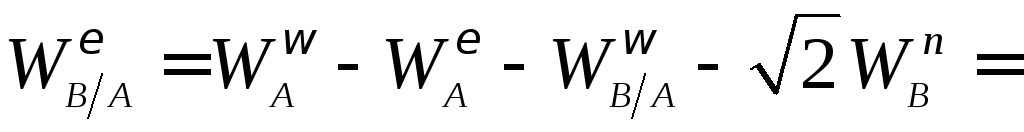
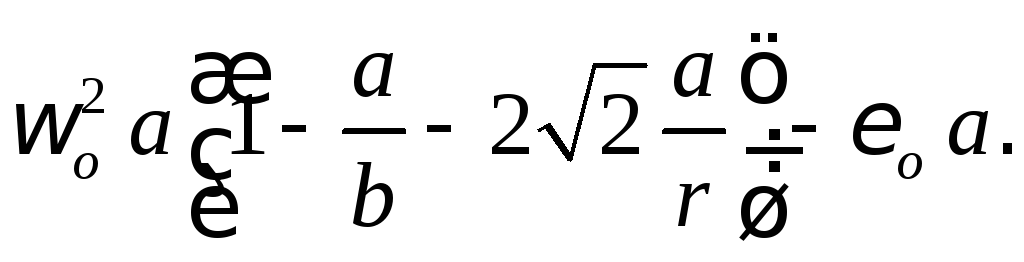
|
Рис. 2.10 |
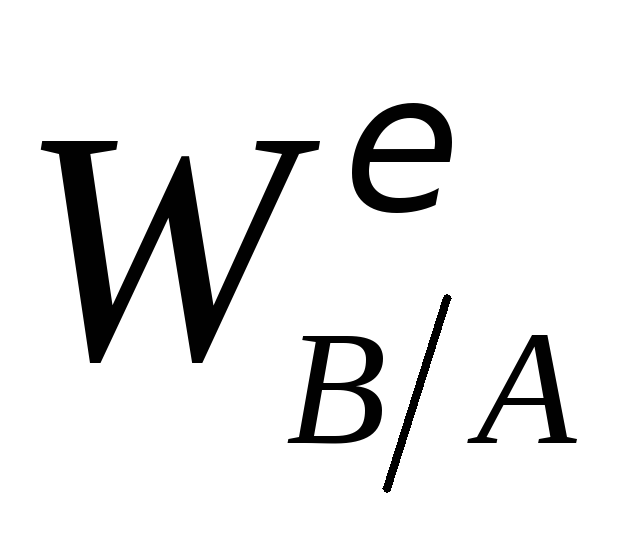 ,
можем определить угловое ускорение
стержня
,
можем определить угловое ускорение
стержня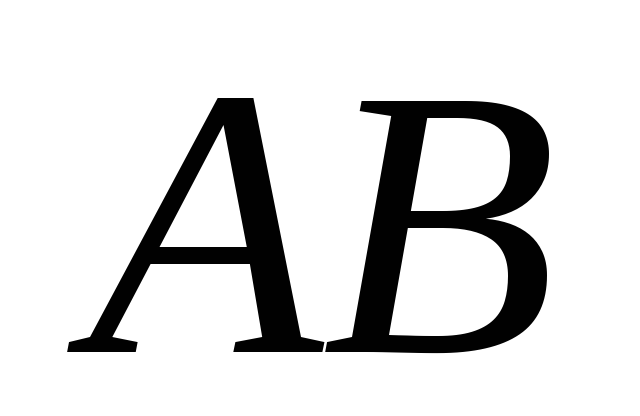 :
: 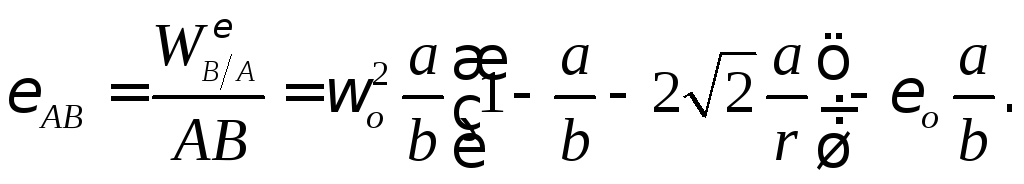
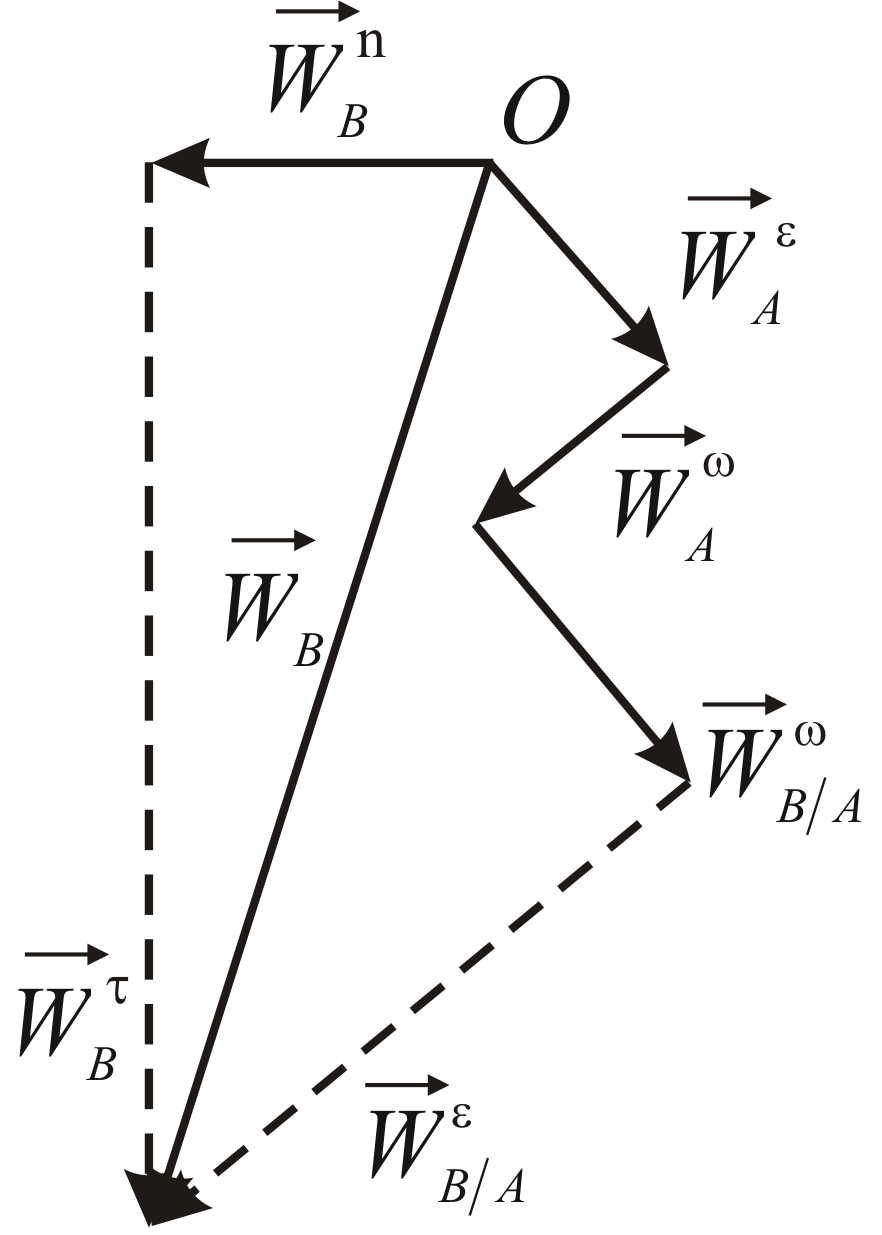
Рассмотрим геометрический способ
решения уравнения  .
Построим в масштабе сумму векторов,
стоящих в правой части уравнения
.
Построим в масштабе сумму векторов,
стоящих в правой части уравнения .
От некоторой точки
.
От некоторой точки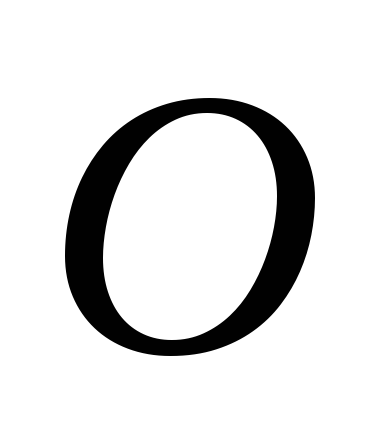 отложим
отложим ,
от его конца отложим
,
от его конца отложим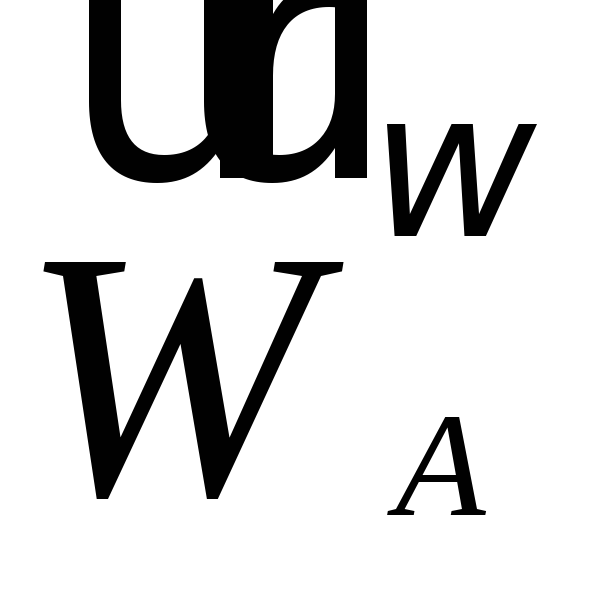 ,
а затем
,
а затем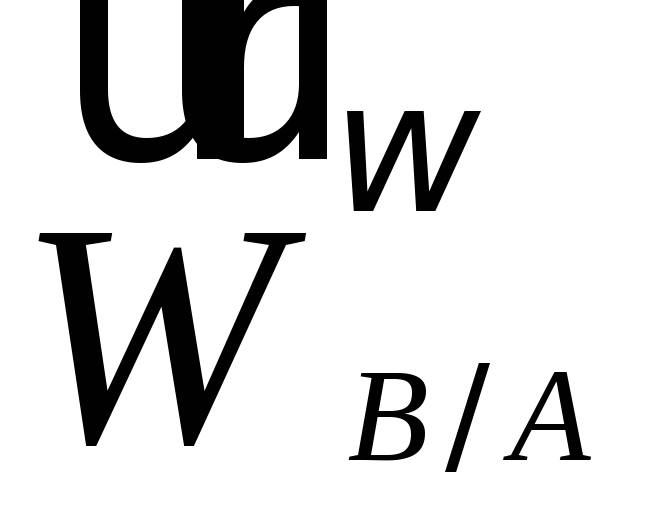 (Рис. 2.10). Остается построить
(Рис. 2.10). Остается построить ,
модуль которого неизвестен. Проведем
через конец
,
модуль которого неизвестен. Проведем
через конец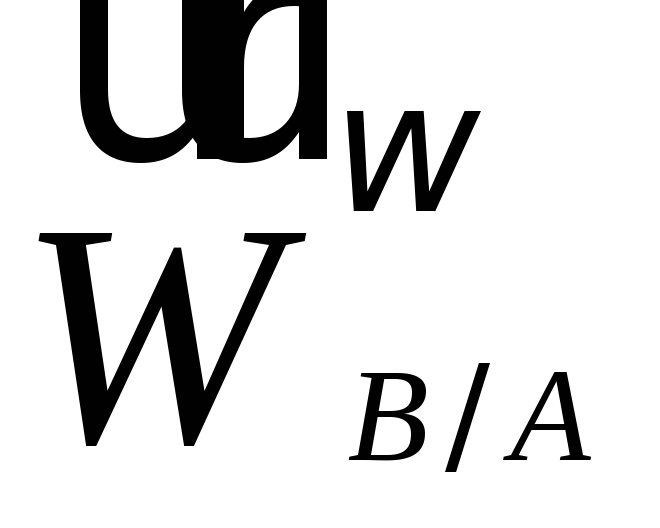 пунктирную прямую, параллельную
пунктирную прямую, параллельную .
Конец суммы векторов, стоящих в правой
части уравнения
.
Конец суммы векторов, стоящих в правой
части уравнения ,
лежит на этой прямой.
,
лежит на этой прямой.
Обратимся к левой части уравнения  .
Отложим от точки
.
Отложим от точки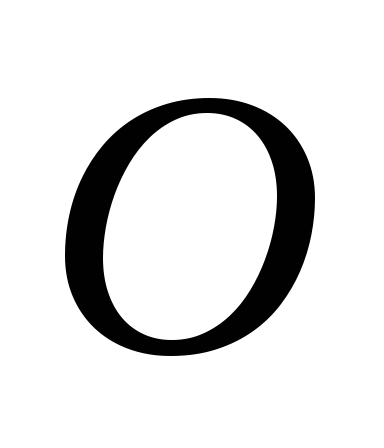 известный вектор
известный вектор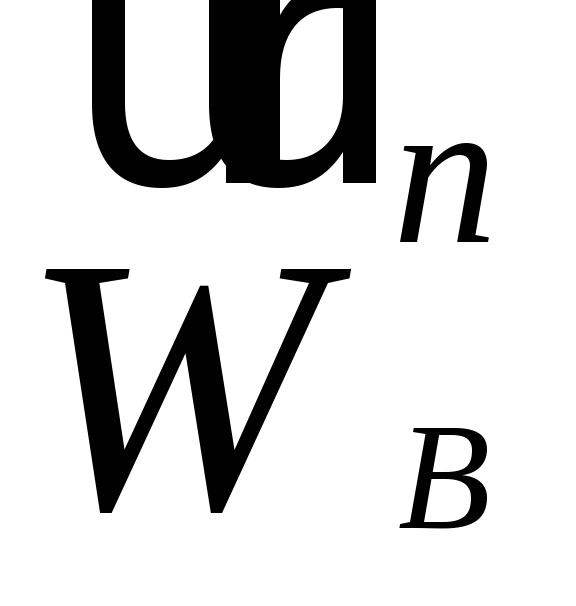 .
Через его конец проведем пунктирную
прямую, параллельную вектору
.
Через его конец проведем пунктирную
прямую, параллельную вектору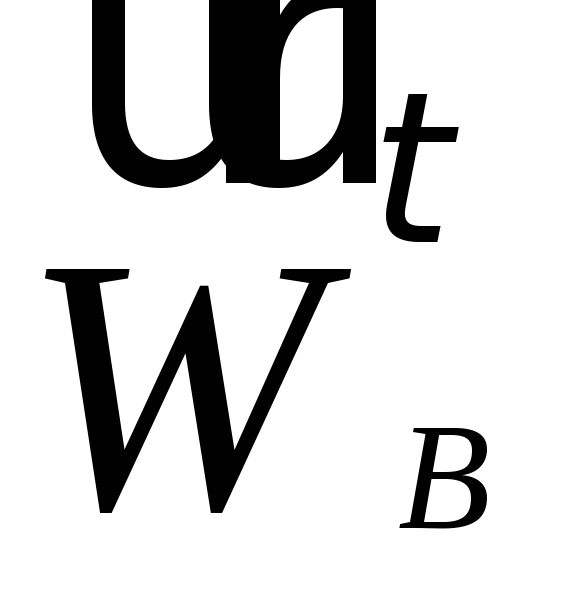 .
Точка пересечения построенных прямых
определяет положение конца вектора
ускорения точки
.
Точка пересечения построенных прямых
определяет положение конца вектора
ускорения точки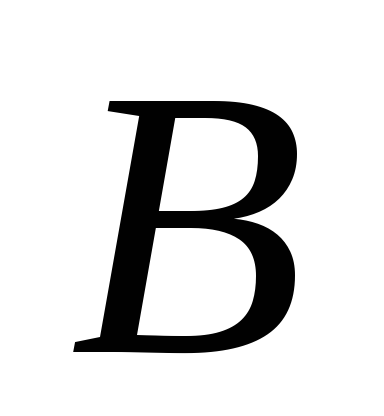 .
.
Пример 2.9
Колесо радиуса
катится без скольжения по прямолинейному
пути (Рис. 2.11). Ось колеса движется
ускоренно, имея в данный момент времени
скорость и ускорение
и ускорение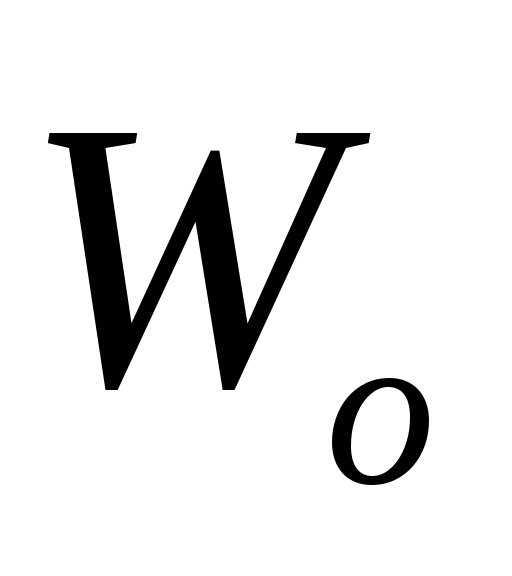 .
Определить проекции ускорение любой
точки
.
Определить проекции ускорение любой
точки обода колеса на оси координат.
обода колеса на оси координат.
Принимая за полюс точку 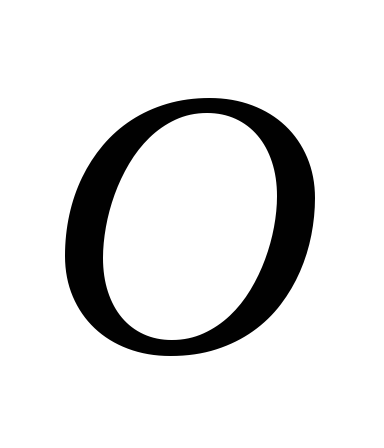 ,
получаем:
,
получаем:
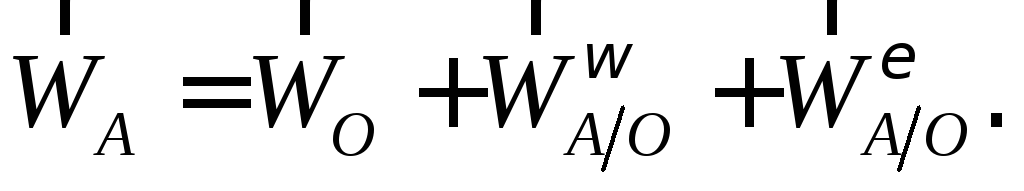

причем
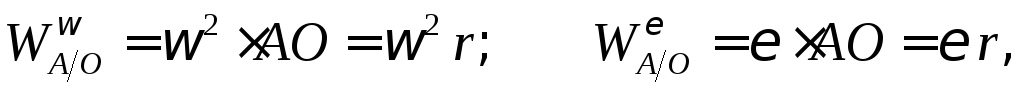
где  – угловая скорость колеса;
– угловая скорость колеса; – его угловое ускорение.
– его угловое ускорение.
|
Рис. 2.11 |
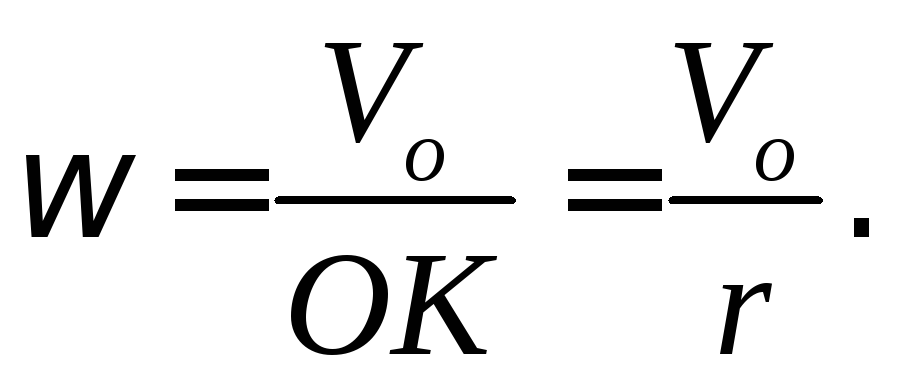
В рассматриваемой задаче расстояние
от точки 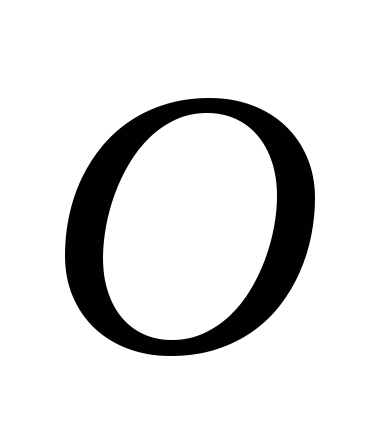 ,
скорость которой известна, до мгновенного
центра скоростей
,
скорость которой известна, до мгновенного
центра скоростей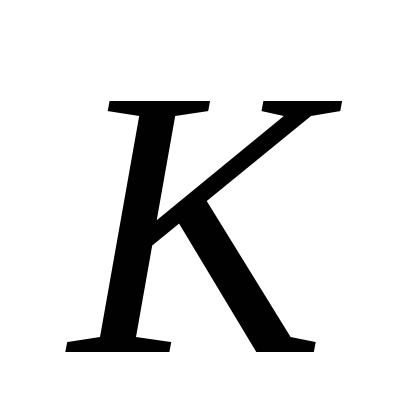 со временем не изменяется. Это
обстоятельство позволяет найти угловое
ускорение колеса в данный момент времени
по определению углового ускорения:
со временем не изменяется. Это
обстоятельство позволяет найти угловое
ускорение колеса в данный момент времени
по определению углового ускорения:
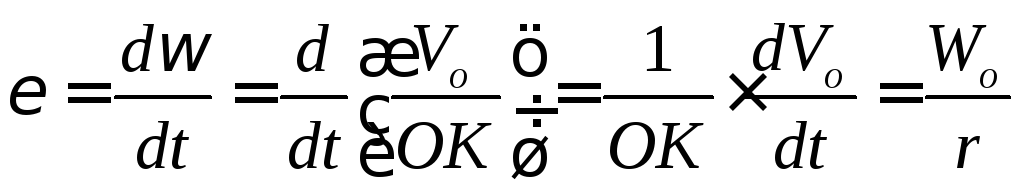 ,
,
так как 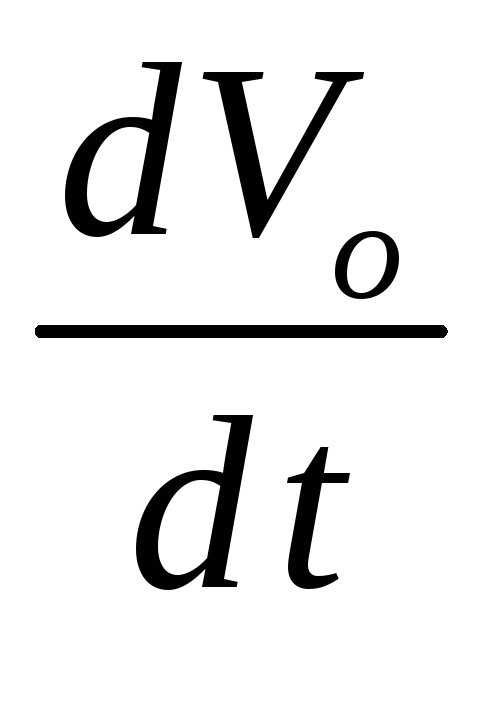 представляет собой проекцию вектора
ускорения точки
представляет собой проекцию вектора
ускорения точки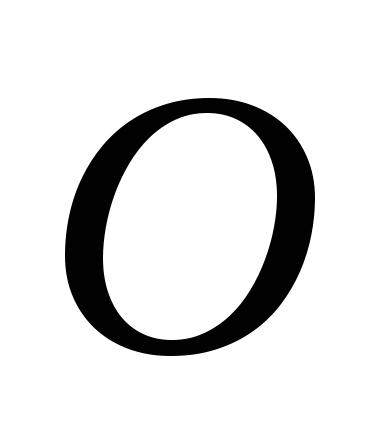 на направление её вектора скорости,
которая в рассматриваемом случае равна
на направление её вектора скорости,
которая в рассматриваемом случае равна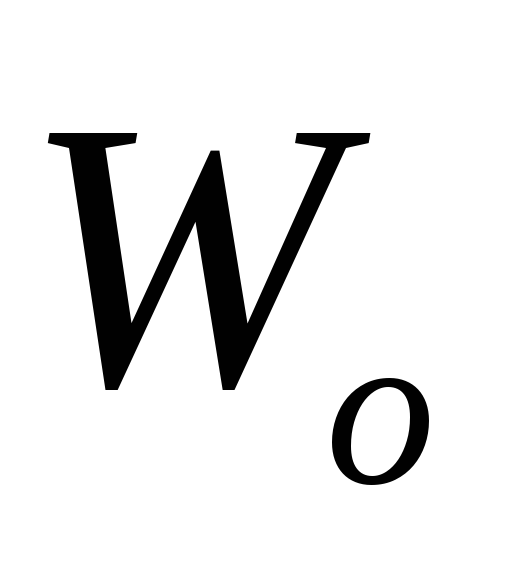 .
.
Записывая уравнение  в проекциях на координатные оси, получаем
проекции вектора ускорения точки
в проекциях на координатные оси, получаем
проекции вектора ускорения точки :
:
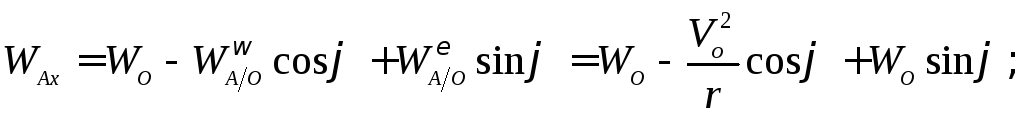
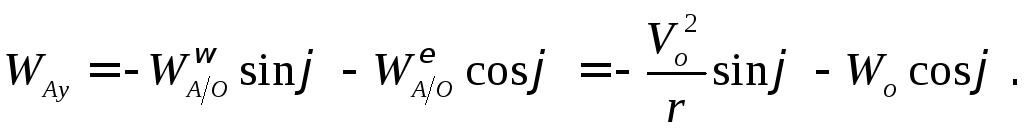
Пример 2.10
Колесо радиуса 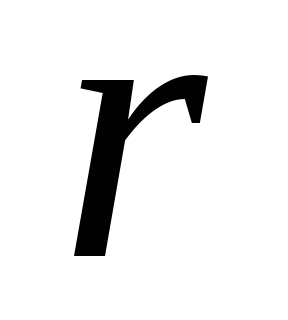 катится без скольжения по криволинейной
поверхности (Рис.2.12). Ось колеса движется
ускоренно, имея в данный момент времени
скорость
катится без скольжения по криволинейной
поверхности (Рис.2.12). Ось колеса движется
ускоренно, имея в данный момент времени
скорость и касательное ускорение
и касательное ускорение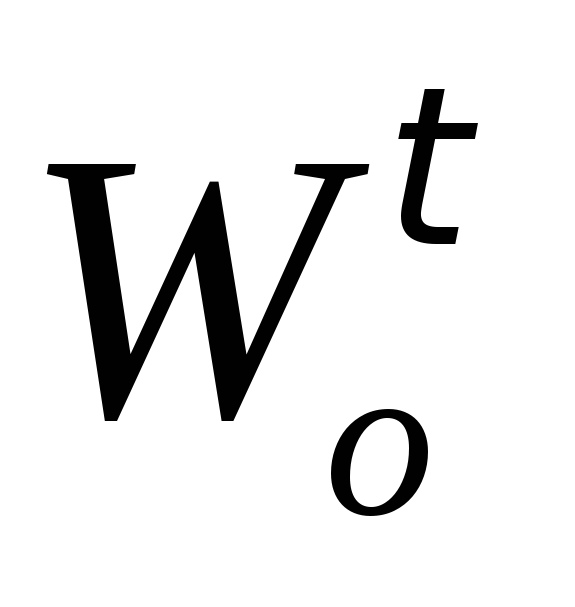 .
Определить проекции ускорения любой
точки
.
Определить проекции ускорения любой
точки обода колеса на заданные координатные
оси, если радиус кривизны в точке
обода колеса на заданные координатные
оси, если радиус кривизны в точке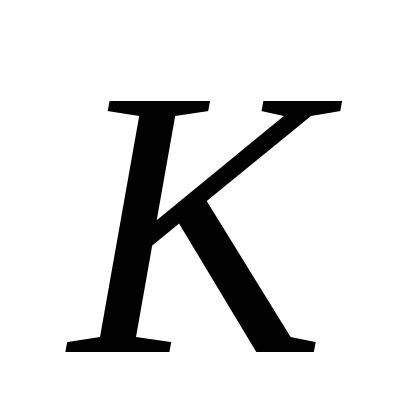 равен
равен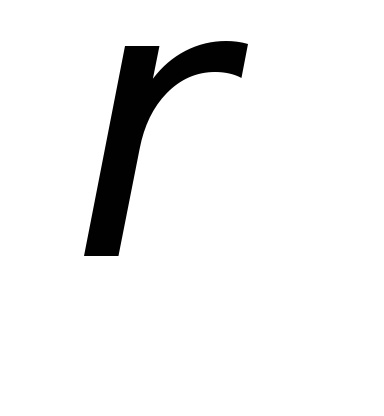 .
.
|
Рис. 2.12 |
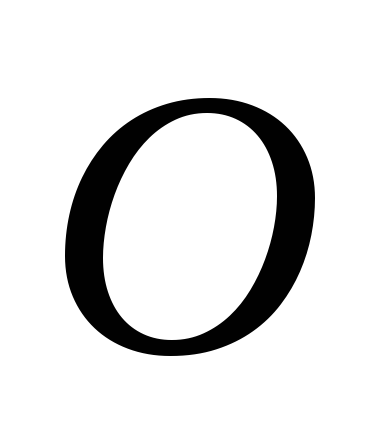 – кривая линия. У точки
– кривая линия. У точки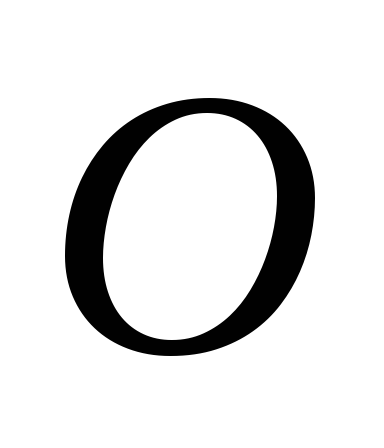 появляется вторая составляющая ускорения
– нормальная:
появляется вторая составляющая ускорения
– нормальная: 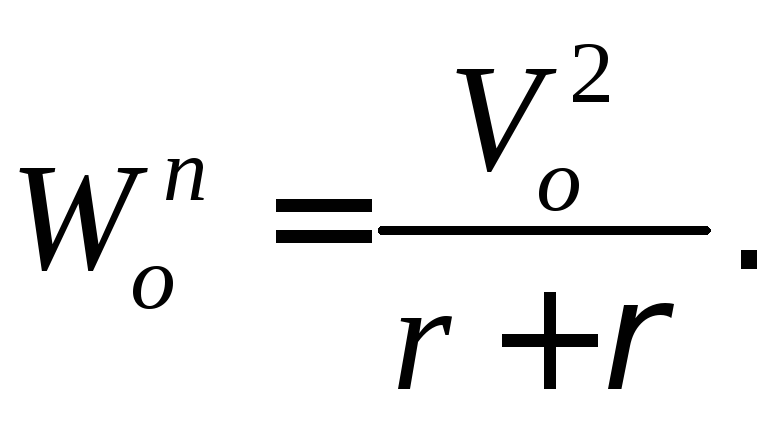
В результате получаем:
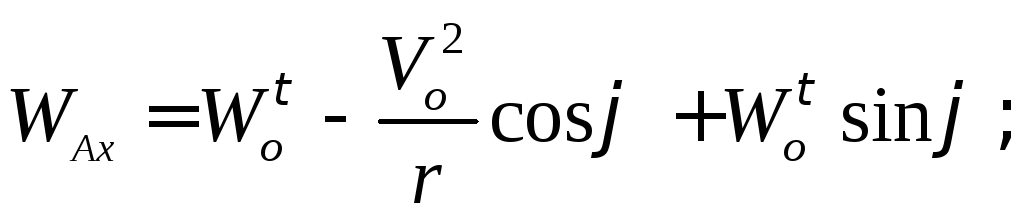
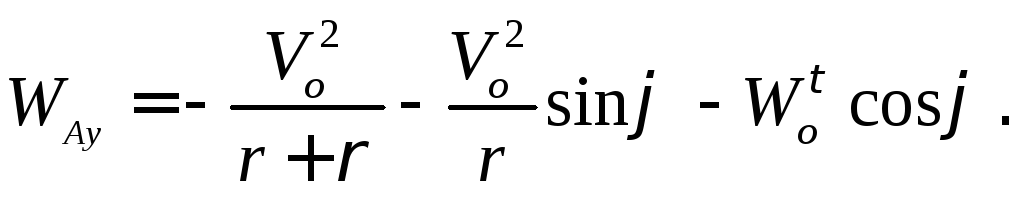
Пример 2.11
Колесо радиуса 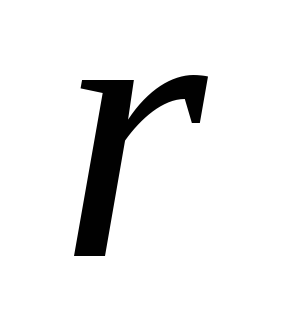 катится без проскальзывания по
прямолинейному пути. Ось колеса движется
равномерно со скоростью
катится без проскальзывания по
прямолинейному пути. Ось колеса движется
равномерно со скоростью (Рис. 2.13). Определить ускорение любой
точки
(Рис. 2.13). Определить ускорение любой
точки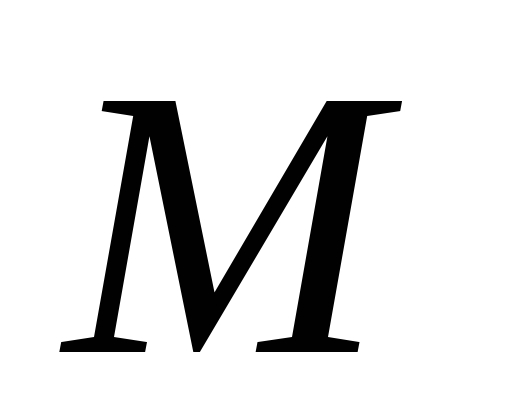 колеса.
колеса.
|
Рис. 2.13 |
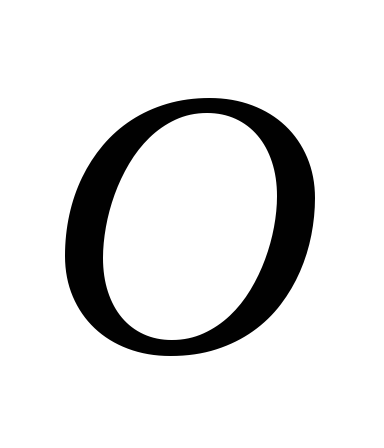 – мгновенный центр ускорений. Для любой
точки
– мгновенный центр ускорений. Для любой
точки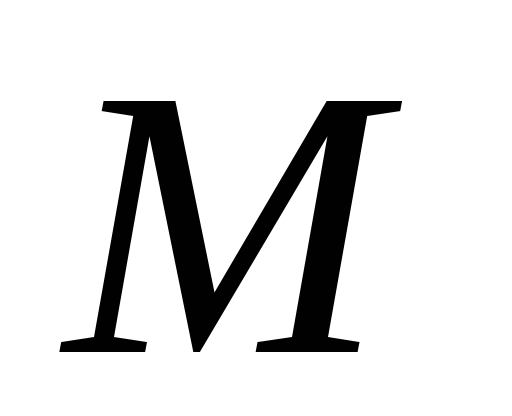 колеса получаем:
колеса получаем: 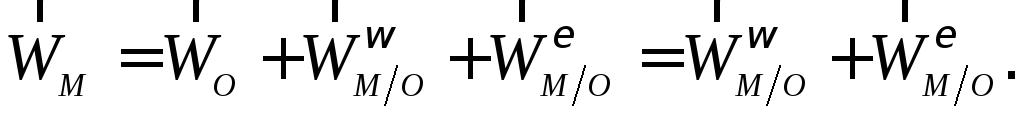
Но угловая скорость колеса 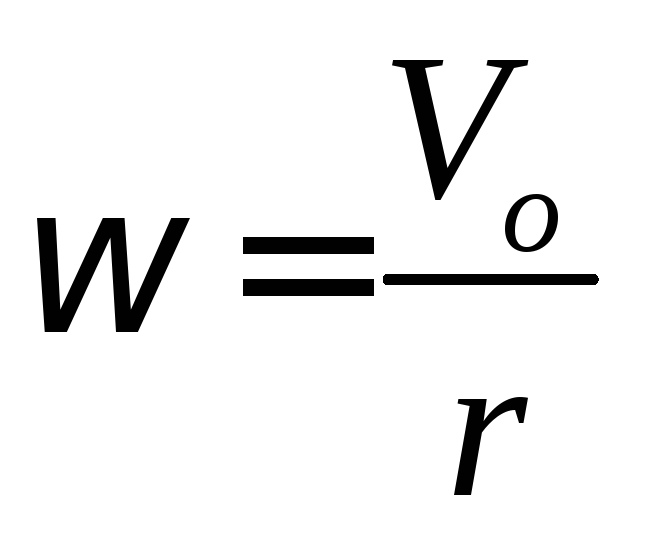 постоянна и, следовательно, угловое
ускорение колеса равно нулю.
постоянна и, следовательно, угловое
ускорение колеса равно нулю.
Тогда
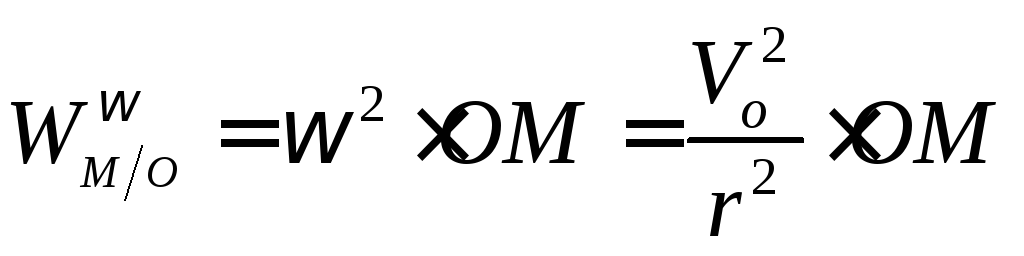
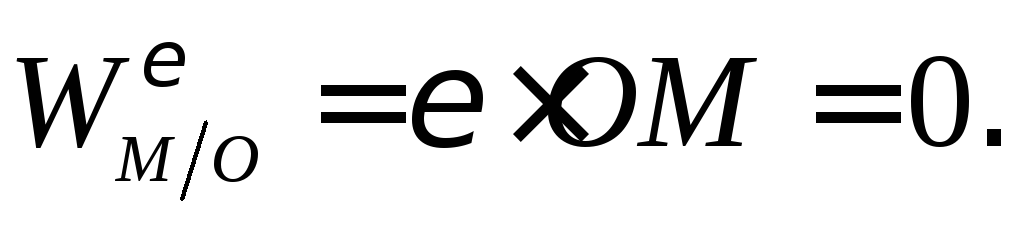
Таким образом, ускорение любой точки
совпадает с осестремительным ускорением,
полученным этой точкой при вращении
колеса вокруг оси, проходящей через
центр колеса  перпендикулярно плоскости движения.
перпендикулярно плоскости движения.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 18.11; 18.13; 18.16; 18.18; 18.22; 18.23; 18.25; 18.26; 18.28; 18.37; 18.38; 18.39; 18.40.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА — теория и практика»: комплекты СР-21;
СР-22.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 7-8
studfile.net
Плоскопараллельное движение.
Плоскопараллельное движение
Понятие о плоскопараллельном движении
Плоскопараллельным движением твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях, параллельных какой-то одной плоскости, называемой основной плоскостью.
Примерами плоскопараллельного движения могут служить движение колеса на прямолинейном участке пути, движение шатуна кривошипно-ползунного механизма.
Из определения плоскопараллельного движения следует, что любая прямая АВ, проведенная в теле перпендикулярно основной плоскости, движется поступательно. Для определения движения тела на каждой прямой, перпендикулярной основной плоскости, достаточно знать движение только одной точки.
Взяв эти точки в одной плоскости, параллельной основной, получим сечение S, движение которого будет определять движение всего тела.
Но плоское движение сечения S вполне может быть определено движением любых двух точек, лежащих в этом сечении. На основании этого можно утверждать, что плоскопараллельное движение тела может быть определено движением отрезка прямой в плоскости, параллельной основной.
Плоскопараллельное движение изучается двумя методами: методом мгновенных центров скоростей и методом разложения плоскопараллельного движения на простейшие движения — поступательное и вращательное.
***
Метод мгновенных центров скоростей
В основе этого метода лежит следующая теорема: всякое плоскопараллельное перемещение твердого тела может быть получено одним вращением около оси, перпендикулярной основной плоскости.
Пусть отрезок, определяющий плоскопараллельное движение тела, за конечный промежуток времени переместился из положения АВ в положение А1В1 (см. рис. 3).
Соединим точки А и А1, В и В1 прямыми линиями и из середин полученных отрезков (точек М и N) восстановим перпендикуляры до их взаимного пересечения в точке О. Эту точку соединим с концами отрезков АВ и А1ВВ1 прямыми линиями, и получим при этом два равных (конгруэнтных) треугольника, имеющих общую вершину О:
Δ АОВ = Δ А1ОВ1.
Треугольник АОВ совмещается с треугольником А1ОВ1 путем поворота на угол φ вокруг точки О, называемой центром конечного поворота.
Точка О есть след оси конечного поворота, перпендикулярной основной плоскости. Таким образом, отрезок АВ, определяющий плоскопараллельное движение тела, перемещается в любое новое положение путем одного вращения вокруг оси конечного поворота.
Теорема доказана.
Приведенное доказательство будет справедливо и в том случае, если перемещение тела произойдет за бесконечно малый промежуток времени Δt.
В пределе при Δt стремящемся к нулю, вращение будет происходить вокруг мгновенной оси, след которой в плоскости фигуры называется мгновенным центром скоростей.
Очевидно, что скорость точки, являющейся в данный момент мгновенным центром скоростей, равна нулю. Угловая скорость ω, с которой происходит мгновенное вращение, называется мгновенной угловой скоростью.
Точка неподвижной плоскости, совпадающая в данный момент времени с мгновенным центром скоростей плоской фигуры, называется мгновенным центром вращения.
Если прямая АВ движется параллельно самой себе, то можно полагать, что тело вращается вокруг оси, удаленной в бесконечность, иначе говоря, поступательное движение можно рассматривать, как вращательное по кругу бесконечно большого радиуса.
Таким образом, плоскопараллельное движение тела может рассматриваться, как непрерывная цепь последовательных мгновенных поворотов вокруг мгновенных осей вращения.
Следует отметить, что методом мгновенных центров скоростей можно пользоваться только для определения скоростей точке плоской фигуры, но не при определении траекторий и ускорений этих точек.
***
Свойства мгновенного центра скоростей
Рассматривая в каждый момент времени сложное плоскопараллельное движение как простейшее — вращательное, можно для вычисления скоростей точек твердого тела применять формулы вращательного движения.
Из закона распределения скоростей точек твердого тела, вращающегося вокруг неподвижной оси, можно установить следующие свойства мгновенного центра скоростей:
- Скорость мгновенного центра скоростей равна нулю;
- Мгновенный центр скоростей лежит на перпендикуляре, восстановленном из точки к направлению ее скорости;
- Скорость точки равна произведению мгновенной угловой скорости на расстояние точки от мгновенного центра скоростей (см. рис. 4): vА = ωОА.
На основании этих свойств можно установить следующие способы определения положения мгновенного центра скоростей плоской фигуры, определяющей плоскопараллельное движение:
1. Если известны мгновенная угловая скорость ω и скорость vА точки А плоской фигуры, то мгновенный центр скоростей будет находиться на перпендикуляре, восстановленном из точки А к вектору скорости vА на расстоянии ОА = vА/ω (см. рис 4).
2. Если известны направления скоростей двух точек А и В плоской фигуры (рис. 5а), то мгновенный центр скоростей будет находиться на точке О пересечения двух перпендикуляров, восстановленных из точек А и В к направлениям их скоростей, причем
vА/vВ = (ωОА)/(ωОВ) = ОА/ОВ,
т. е. скорости точек плоской фигуры прямо пропорциональны их расстояниям от мгновенного центра скоростей.
3. Если известно, что скорости двух точек А и В плоской фигуры параллельны друг другу, направлены в одну сторону, перпендикулярны отрезку АВ и по модулю не равны (рис. 5б), то мгновенный центр скоростей О будет находиться в точке пересечения прямой, соединяющей начала векторов vА и vВ с прямой, соединяющей концы этих векторов.
Если векторы скоростей А и В равны между собой, то мгновенный центр скоростей в данный момент времени находится в бесконечности, мгновенная угловая скорость ω равна нулю, скорости всех точек плоской фигуры будут одинаковы и движение будет мгновенно поступательным.
4. Если скорости двух точек А и В плоской фигуры параллельны друг другу, направлены в противоположные стороны и перпендикулярны отрезку АВ (см. рис. 5в), то мгновенный центр скоростей О будет находиться в точке пересечения отрезка АВ с прямой, соединяющей концы векторов vА и vВ.
5. Если плоская фигура катится без скольжения по неподвижной кривой, мгновенный центр скоростей О будет находиться в точке соприкосновения фигуры с кривой, так как скорость этой точки фигуры относительно кривой равна нулю (скольжение отсутствует).
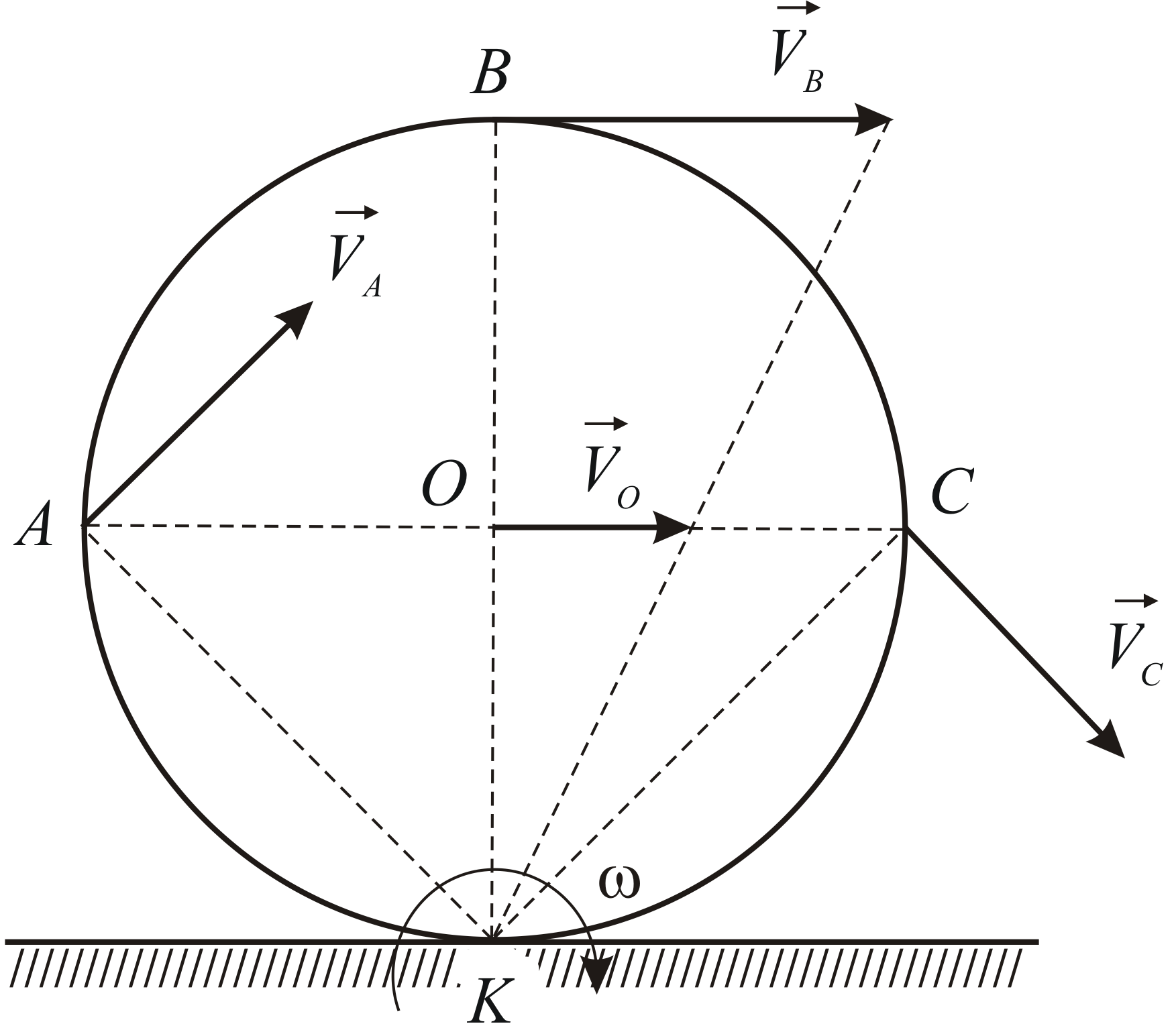
На рис. 6 приведены положения мгновенного центра скоростей (МЦС) и графики скоростей точек вертикального диаметра колеса при различных случаях его качения по прямолинейному рельсу (скольжение, качение, буксование и т. п.).
***
Разложение плоскопараллельного движения на вращательное и поступательное
В основе этого метода лежит следующая теорема: всякое плоскопараллельное перемещение твердого тела может быть получено с помощью одного вращательного и одного поступательного движения.
Пусть за время Δt отрезок АВ, определяющий плоскопараллельное движение тела, переместился в положение А1В1. Предположим, что отрезок АВ вначале перемещался только поступательно, причем все его точки двигались одинаково, как, например, точка А. Таким образом, отрезок переместился в положение А1В2, после чего его можно переместить в положение А1В1 посредством только вращательного движения вокруг точки А1.
Очевидно, что сложное плоскопараллельное движение состоит из двух простейших движений – поступательного и вращательного, причем можно считать, что эти движения совершаются одновременно.
Установим зависимость между векторами скоростей точек А и В. Для этого соединим прямыми точки А, А1 и В, В1, в результате чего получим следующую зависимость между векторами перемещений точки В:
ВВ1 = ВВ2 + В2В1.
Так как ВВ2 = АА1, то можно записать, что ВВ1 = АА1 + В2В1.
Разделим все члены равенства на Δt и перейдем к пределу при Δt стремящемся к нулю:
lim (ВВ1)/Δt = lim (АА1τ)/Δt + lim (В2В1)/Δt, откуда получим: vВ = vА + vВА,
где vА и vВ – векторы абсолютных скоростей соответствующих точек, vВА – вектор скорости точки В в относительном вращательном движении отрезка АВ вокруг точки А, направленный перпендикулярно отрезку АВ.
Таким образом, плоскопараллельное движение тела может осуществляться путем одновременно происходящих вращательного и поступательного движений; поступательное движение можно считать переносным, а вращательное – относительным.
Вектор абсолютной скорости произвольной точки В равен вектору абсолютной скорости любой другой точки А плюс вектор скорости точки В в относительном вращательном движении отрезка АВ вокруг точки А.
Точку, вокруг которой происходит относительное вращательное движение, называют полюсом.
Если за полюс вместо точки А принять точку В, то, рассуждая аналогично, получим:
vА = vВ + vВА.
Если сравнить это векторное равенство с предыдущим, становится очевидным, что векторы относительных скоростей vВА и vАВ по модулю равны между собой, т. е. vВА = vАВ.
Из рис. 7 видно, что направление относительного вращения и угол поворота отрезка АВ за какой-то промежуток времени не зависит от выбора полюса, т. е. φВА = φАВ.
Продифференцировав это равенство по времени, получим:
dφВА/dt = dφАВ/dt или ωВА= ωАВ.
Следовательно, относительная угловая скорость от выбора полюса не зависит. Аналогичный вывод можно сделать и об относительном угловом ускорении:
dωBA/dt = dωAB/dt или αВА= αАВ.
На основании вышеизложенного можно сделать вывод, что при разложении плоскопараллельного движения на поступательное и вращательное поступательная составляющая движения в общем случае зависит от выбора полюса, а вращательная составляющая от выбора полюса не зависит.
Так как за полюс может быть выбрана любая точка плоскости, в том числе и мгновенный центр скоростей, то при разложении плоскопараллельного движения на поступательное и вращательное угловая скорость относительного вращательного движения всегда равна абсолютной угловой скорости.
Если векторное равенство vА = vВ + vАВ спроецировать на направление прямой АВ, то получим, что проекция vА равна проекции vВ, так как проекция vАВ равна нулю. Следовательно, при плоскопараллельном движении проекции скоростей двух точек плоской фигуры на направление прямой, соединяющей эти точки, равны между собой.
***
Динамамика материальной точки
k-a-t.ru
Слободянюк А.И. Физика 10/3.6 — PhysBook
Содержание книги
Предыдующая страница
§3. Криволинейное движение. Плоскопараллельное движение твердого тела
3.6 Плоскопараллельное движение
Движение твердого тела называется плоскопараллельным, если траектории движения всех его точек являются плоскими кривыми, лежащими в параллельных плоскостях.
Плоскопараллельное движение твердого тела можно представить как суперпозицию поступательного движения и вращения вокруг оси, направление которой не изменяется. Наглядными примерами такого движения являются качение колеса, движение книги без отрыва от стола и т.д.
Для описания положения абсолютно твердого тела при плоскопараллельном движении необходимо задать две декартовые координаты какой-либо точки тела [1] и угол его поворота, то есть плоскопараллельное движение обладает тремя степенями свободы.
Выберем внутри тела две точки A, B; зададим координаты xA, yA точки A и угол φ, который образует отрезок AB с направлением оси X. Три числа xA, yA и φ однозначно определяют положение тела на плоскости, следовательно, являются его координатами. Зная эти координаты, можно определить положение в пространстве любой другой точки твердого тела путем геометрических построений.
Покажем теперь, как можно найти скорость любой точки твердого тела при плоскопараллельном движении (рис. 36).
Разложим движение на две составляющих — поступательное движение, скорость которого обозначим \(~\vec V\) , и вращение вокруг оси, проходящей через точку A, с угловой скоростью \(~\omega = \frac{\Delta \varphi}{\Delta t}\) . Тогда скорость любой другой точки тела (например, B) является векторной суммой скоростей поступательного и вращательного движений —
\(~\vec V_B = \vec V + \vec V_{BP}\) , (1)причем вектор скорости вращательного движения направлен перпендикулярно отрезку AB и равен по абсолютной величине VBP = ωr, где r расстояние от точки B до оси вращения.
Рассмотрим катящееся без проскальзывания колесо радиуса R (рис. 37).
Пусть его центр движется со скоростью \(~\vec V\). Найдем скорости некоторых других точек колеса. Для этого представим движение колеса как сумму поступательного движения его центра и вращения вокруг его оси. Так как движение происходит без проскальзывания, то угловая скорость вращения определяется формулой \(~\omega = \frac{\upsilon}{R}\). Для точек, находящихся на ободе колеса линейная скорость вращательного движения равна по модулю скорости поступательного движения, так как для них расстояние до оси вращения равно радиусу колеса, поэтому \(~V_{BP} = \omega r = \frac{V}{R} R = V\) . Однако, направление этой скорости различно для разных точек. Так, для точки A скорость вращательного движения направлена горизонтально, также как и скорость поступательного движения. Поэтому суммарная скорость точки A равна 2V и направлена горизонтально. Скорость вращательного движения точки B направлена вертикально вверх, поэтому ее полная скорость направлена под углом 45° к горизонту, а ее модуль \(~V_B = V \sqrt{2}\) . Очень интересна точка касания с поверхностью C : скорость ее вращательного движения направлена горизонтально в сторону противоположную скорости поступательного движения, поэтому ее полная скорость равна нулю.
Так как разложение движения на составляющие не является однозначным, можно теперь представить качение колеса как сумму движения точки C и вращения вокруг оси, проходящей через эту точку. Мы показали, что скорость точки C равна нулю, поэтому появляется возможность рассматривать движение колеса как чистый поворот вокруг точки C. Правда, это возможно в течение только бесконечно малого промежутка времени, потому, что в следующий момент точкой касания будет другая точка колеса. Множество точек твердого тела, скорости которых в данный момент равны нулю, образуют мгновенную ось вращения тела. Такая ось существует при любом движении твердого тела. Правда положение этой оси постоянно изменяется, поэтому для вычисления координат точек такое представление движения не дает особых преимуществ. Но для вычисления скоростей точек, рассматривать плоскопараллельное движение как чистый поворот очень удобно.
Легко доказать, что угол поворота тела не зависит от того, относительно какой оси мы его рассматриваем, следовательно, и угловая скорость не зависит от оси. С этой точки зрения, скорость любой точки колеса определяется формулой V = ωr’ , где r’ — расстояние от данной точки до мгновенной оси вращения.
Рассмотренная задача об определении скоростей точек катящегося колеса может быть легко решена, если рассматривать его движение как поворот вокруг точки C (рис. 38): точка A находится на расстоянии 2R от мгновенной оси вращения, поэтому ее скорость равна VA = 2Rω = 2V; точка B находится на расстоянии \(~R \sqrt{2}\) от оси, ее скорость \(~V \sqrt{2}\). Направления векторов скоростей также совпадают с полученными ранее.
Таким образом, мы имеем два примерно одинаковых по сложности способа описания движения твердого тела: первый — суперпозиция поступательного и вращательного движений: второй — поворот вокруг мгновенной оси.
Примечания
- ↑ С точки зрения кинематического описания выбор этой точки произволен — только следует стремиться к тому, чтобы траектория этой точки была попроще. Далее мы укажем как можно легко найти такую точку.
Следующая страница
www.physbook.ru
Как движется автомобиль — Энциклопедия журнала «За рулем»
Многие из нас встречали картинку: улица прошлого века, и на мостовой — экипаж без лошадей. Такими примерно были «самобеглые коляски» русских изобретателей Шамшуренкова и Кулибина. Катил «самобеглую» стоявший на педалях человек. Его «механическая энергия » передавалась на ведущие колеса, которые и толкали коляску. Этот же принцип лег в основу другого «самодвижущегося экипажа», появившегося позднее, — автомобиля. Только источником механической энергии у него стал двигатель внутреннего сгорания. Как же его энергия приводит в движение автомобиль?
Где толкающая сила?
Рычаг-помощник
Откуда же она возникает, если автомобиль не толкают как тележку и его не тянет лошадь?
Чтобы ответить на этот вопрос, давайте разберем способ, которым можно тележку передвигать, — при помощи рычага. А чтобы нижний конец его не скользил, — забьем в землю клин.
Первый вариант — толкаем рычагом непосредственно тележку. Она сдвинется и в том случае, когда рычаг воздействует прямо на ось колеса, причем плечо, на которое действует рука, получается вдвое большим. Эту работу можно облегчить — придавить рычаг с такой силой, чтобы, опираясь на дорогу, его нижний конец не проскальзывал. Останется лишь непрерывно переставлять его.
А если прилагать силу к верхней части колеса по касательной к окружности? Тогда полоску, выделенную на рисунке посредине пунктиром, можно рассматривать как такой же рычаг, вес машины прижимает ведущее колесо к дороге — оно не пробуксовывает, значит, нижний конец нашего «рычага» как бы удерживается колышком и ось колеса переместится под действием силы F.
Когда ось продвинется несколько вперед — колесо провернется и «конец рычага» — точка 1 уже не будет соприкасаться с дорогой. Ее место займет точка 2, затем точка 3 и так далее.
Таким образом, колесо можно рассматривать как бы состоящим из бесконечного числа рычагов, непрерывно и последовательно сменяющих один другой. Оно удобнее рычага — ничего не нужно переставлять. Способ перекатывания повозки за обод колеса применяют, когда надо помочь лошади. Подобным образом поступают и артиллеристы, выкатывая вручную орудия на огневые позиции: это легче, ибо усилие на оси получается вдвое большим, чем в том случае, если толкать за станину.
Однако лучше не толкать и не тянуть колесо, а вращать. Так нельзя ли найти такой способ, чтобы не толкать и не тянуть колесо, перехватывая его все время за обод? Можно. Для этого достаточно передавать на колесо через ось вращающее усилие, или, как принято говорить в технике, подвести к нему крутящий момент. Крутящий момент стремится провернуть колесо, но этому препятствует сила трения, возникающая между ним и дорогой. Колесо как бы отталкивается от земли и начинает катиться. Здесь главный помощник — трение, без него движение невозможно. Известно, как беспомощен автомобиль, например, на льду.
Разные дороги и разные силы
Все — «против»
По асфальту тележка катится легко. Но вот колеса попали на мягкий грунт или песок. Толкать ее,стало труднее. B чем дело? Возросла сила, которую в теории автомобиля называют силой сопротивления качению.
А если встретится подъем? Добавляется сила, стремящаяся скатить тележку.
А встречный ветер? Каждый из нас знает, как трудно двигаться, когда он сильный. Но мчащийся автомобиль сам ‘«устраивает» себе искусственный встречный ветер, и тем сильнее, чем больше скорость.
Кроме того, при разгоне тележку приходится толкать намного сильнее, чем при. равномерном движении: нужно преодолевать силы инерции.
Итак, автомобиль равномерно движется по хорошей горизонтальной дороге: нужна умеренная толкающая сила — лишь для того, чтобы преодолевать трение и сопротивление воздуха.
Но ведь сначала надо тронуться с места. А для этого требуется самая большая толкающая сила. Хотим ускорить движение — надо преодолеть инерцию, опять, же необходимо увеличение толкающей силы. Съехали на плохую дорогу или поднимаемся в гору. И здесь толкающая сила должна намного возрасти. Обычно в зависимости от условий движения она меняется в несколько раз. Соответственно должен меняться и подводимый к колесам крутящий момент. Мы видим: чтобы автомобиль мог двигаться по различным дорогам и с разной скоростью, надо иметь возможность увеличивать и уменьшать крутящий момент на его колесах в широких пределах.
Упрямый характер
От двигателя — и колесам
Скорость вращения коленчатого вала двигателя внутреннего сгорания может изменяться примерно от пятисот, когда он работает на «холостом ходу», до нескольких тысяч оборотов в минуту. Казалось бы, можно двигаться с различной скоростью, даже если мотор непосредственно соединить с колесами: быстрее вращается вал двигателя — и, пожалуйста, с большей скоростью идет машина.
У бензинового «характер» хуже
Но вот дорога пошла в гору, и сразу автомобильный двигатель показывает свой «характер». Он значительно снижает обороты (труднее стало тянуть), но крутящий момент увеличивается недостаточно: на десять процентов, на тридцать, самое большое — на пятьдесят. У дизельных двигателей такая «приспособляемость» еще хуже. Давайте взглянем на график. Он показывает, как меняется величина крутящего момента бензинового автомобильного двигателя. Видно и самое худшее: с какого-то числа оборотов (в этом месте поставлена галочка) крутящий момент непрерывно уменьшается.
Действительно, при снижении числа оборотов с 4500 до 3000 крутящий момент возрос с 7 до 9 кгм. Но если подъем, допустим, потребовал большего, двигатель внутреннего сгорания не может справиться с этой задачей: необходимо увеличение момента, а он начинает уменьшаться, скорость движения резко падает — обороты двигателя идут на убыль… крутящий момент становится еще меньше…
В том же диапазоне чисел оборотов современного тягового электродвигателя крутящий момент увеличивается примерно в четыре раза.
В этом отношении для автомобиля больше подошли бы двигатели паровые или электромоторы, как бы отвечающие золотому правилу механики: при большой нагрузке они сбавляют обороты, а тянут сильнее. Но двигатель плюс котельная установка слишком громоздки для автомобиля, а возить на нем электростанцию просто невозможно. Двигатель же внутреннего сгорания обладает пока многими другими преимуществами. А на его «дурной характер» можно найти управу.
Выход есть!
Можно и быстро и медленно
Силы человека, работавшего на педалях «самобеглой» коляски, хватало на движение по ровной дороге. А на подъеме? Для его преодоления между «двигателем» и ведущими колесами был помещен специальный зубчатый барабан. Он позволял увеличить крутящий момент, подводимый к колесам, за счет скорости их вращения, — а следовательно, и скорости движения коляски. Крутящий момент увеличивался, когда ведущая шестерня соединялась с рядом зубьев барабана, расположенных дальше от оси (наибольшее плечо) и, наоборот, — уменьшался при укорочении плеча.
Так же меняется величина крутящего момента и в шестеренчатой передаче, распространенной в современной технике.
И вперед и назад
Менять величину крутящего момента двигателя может механизм, в котором будет несколько пар зацепленных одна с другой шестерен, — допустим, три — с различными передаточными числами: 1:4; 1:2 и 1:1. Первые два позволяют увеличить крутящий момент (толкающую силу) в четыре или в два раза.
Схема такого механизма — коробки передач — показана на рисунке. В общем корпусе находятся три пары шестерен с разными передаточными числами. Шестерни ведомого вала, через который вращение передается к колесам, могут передвигаться вдоль него, все время вращаясь с ним. Действуя рычагом переключения, водитель может соединить любую пару и двигаться на любой из трех передач. Это первая услуга коробки.
Вторая услуга. На рисунке коробка показана в положении «включена первая передача». Если расцепить и эту пару — вращение от двигателя к колесам передаваться не будет. Такое положение называется нейтральным.
При нейтральном положении двигатель не соединен с колесами, и поэтому его легко пустить, прогреть, не надо выключать при остановке перед светофором и т. п.
Третья услуга. Даже мотоцикл случается подать назад. Автомобилю — это просто необходимо. Надо и развернуться и встать под погрузку, подъехать к прицепу…
В общем, ведущие колеса должны вращаться и назад. А двигатель? Его коленчатый вал вращается только в одну сторону. Значит, коробка должна иметь передачу заднего хода. Между ведущим и ведомым валами в зацепление вводится «лишняя» шестерня или две на общей оси, как показано на рисунке. Она и меняет направление вращения ведомого вала.
Чтобы трогаться плавно
Вот теперь плавно!
Просто соединить шестерни первой передачи не удастся — одна вращается, другая неподвижна. А если включить передачу принудительно — машина «прыгнет» вперед или заглохнет двигатель, да и для зубьев шестерен это небезопасно.
Избавиться от таких неприятностей и плавно тронуться с места позволяет особый механизм — «сцепление», которое располагают между двигателем и коробкой. Оно имеет два положения: сцепление
включено — крутящий момент передается на коробку; сцепление выключено — она отсоединена от двигателя.
Для передачи вращения здесь используется сила трения между маховиком и ведомым диском. Расположенные по окружности пружины прижимают диск к маховику, и он вращается вместе с ним — сцепление включено. В таком положении оно находится при движении автомобиля. Пружины обеспечивают такую силу трения, которая необходима для передачи крутящего момента двигателя, без пробуксовки
между маховиком и ведомым диском.
Когда водитель нажмет ногой на левую педаль (так принято на автомобилях всего мира), диск, преодолевая усилие пружин, отходит от маховика. Мы говорим: сцепление выключено. Передача крутящего
момента от двигателя прекращается, хотя его коленчатый вал и маховик продолжают вращаться.
В таком положении — педаль нажата — водитель включает передачу и, плавно отпуская педаль, постепенно приближает ведомый диск к гладкой поверхности маховика. В это время общая сила давления пружин все увеличивается и сила трения возрастает. Маховик постепенно, плавно увлекает диск, который со все уменьшающимся проскальзыванием начинает вращаться, и… машина плавно трогается. Успех этого процесса зависит от искусства водителя, поначалу частенько он проходит не совсем гладко.
Когда нужно переключить передачу — «перейти», например, при разгоне с первой на вторую или со второй на третью — водитель каждый раз нажимает на педаль сцепления.
wiki.zr.ru
4 Кинематика и динамика автомобильного колеса » СтудИзба
План лекции
3.1. Общие сведения
3.2. Упугое проскальзывание и скольжение колеса. Радиус качения колеса.
3.3. Момент сопротивления качению эластичного колеса в ведомом режиме
3.4. Влияние конструктивных и эксплутационных факторов на коэффициент сопротивления качению
3.1.Общие сведения
Энергия вращения, вырабатываемая двигателем автомобиля, преобразуется в поступательное движение транспортного средства движетелем, в качестве которого в автомобиле выступает система колес с эластичными пневматическими шинами.
Пневматическая шина представляет собой оболочку, наполненную сжатым воздухом. При качении колеса по дороге происходит деформация этой оболочки и проскальзывание элементов протектора относительно поверхности дороги.
Размер автомобильного колеса в свободном, ненагруженном состоянии характеризуется свободным радиусом rc. Свободный радиус колеса — половина наружного диаметра Dн;
rc =0.5 Dн.
Под наружным диаметром колеса понимается диаметр наибольшего окружного сечения беговой дорожки колеса при отсутствии контакта с дорогой. Наружный диаметр колеса зависит от давления воздуха в шине и, как правило, возрастает с его увеличением, определяется непосредственно замером. Значение наружного диаметра колеса при номинальном давлении воздуха в шине указывается в ГОСТах или каталогах.
При действии на колесо вертикальной нагрузки происходит деформация части шины, соприкасающейся с опорной поверхностью. При этом расстояние от оси колеса до опорной поверхности становится меньше свободного радиуса. Это расстояние, замеренное у неподвижного колеса, называется статическим радиусом rст. Статический радиус при номинальных нагрузках и давлении воздуха в шинах также указывается в их характеристиках. Обычно шины конструируют таким образом, чтобы при номинальных нагрузке и давлении прогиб шины составлял 13… 20 % от высоты профиля. Статический радиус при известных конструктивных параметрах шин можно находить из соотношения:
rст =0,5d+lzH,
где d — посадочный диаметр обода шины;
lz —коэффициент вертикальной деформации, зависящий от типа шин:
для тороидных шин lz =0,85…0,87;
для шин с регулируемым давлением и арочных lz =0,8…0,85;
Н — высота профиля.
При качении нагруженного колеса в силу ряда причин (динамическое действие нагрузки, передаваемый колесом крутящий момент, скорость вращения и др.) расстояние между осью колеса и опорной поверхностью меняется. Это расстояние называют динамическим радиусом rд. При качении колеса по твердой опорной поверхности с малой скоростью статический и динамический радиусы его практически одинаковы. Поэтому при приближенных расчетах динамический радиус часто принимают равным статическому.
3.2. Упугое проскальзывание и скольжение колеса. Радиус качения колеса.
Реальное автомобильное колесо в тангенциальном направлении не является абсолютно жестким. Под воздействием передаваемого крутящего момента протектор деформируется в тангенциальном направлении. Если направление передаваемого момента совпадает с направлением угловой скорости колеса, элементы шины, находящиеся в набегающей полуокружности, подвергаются сжатию, а с противоположной стороны — растяжению, как это показано на рис. 3.4. На этом же рисунке показана эпюра тангенциальных напряжений в протекторе шины.
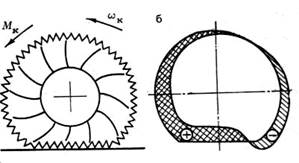
Рис. 3.4. Деформация шины (а) и эпюра напряжений в протекторе (б) при приложении к колесу крутящего момента:+ —зона сжатия; — —зона растяжения
Элементы шины, находящиеся в контакте с опорной поверхностью, нагружены в тангенциальном направлении неодинаково: элементы, входящие в контакт, сжимаются, а выходящие — растягиваются. При возрастании передаваемого крутящего момента увеличивается площадь, в пределах которой происходит проскальзывание шины относительно дороги (рис. 3.5).
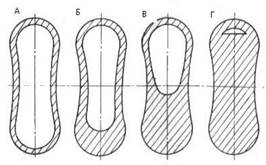
Рис. 3.5. Зависимость площади скольжения колеса (заштрихованная зона) от передаваемого им момента Мк
При некотором значении момента начинается одновременное перемещение всех находящихся в зоне контакта точек колеса. Перемещение части точек колеса, находящихся в контакте с дорожным покрытием, относительно опорной поверхности, когда в зоне контакта есть точки, неподвижные относительно этой поверхности, называется упругим проскальзыванием колеса. Одновременное же перемещение всех находящихся в контакте точек колеса называется скольжением колеса.
Вследствие упругого проскальзывания или скольжения путь, проходимый колесом за один оборот, оказывается меньшим, чем путь, проходимый в ведомом режиме. При возрастании передаваемого крутящего момента увеличивается тангенциальная деформация шины и скольжение, а путь, проходимый колесом за один оборот, уменьшается.
Радиус качения колеса можно представить как радиус условного недеформируемого кольца, которое, катясь без скольжения, совершит число оборотов и пройдет путь, одинаковый с реальным колесом. Радиус качения колеса является условной величиной и непосредственно не связан с его размерами. Он определяется как отношение поступательной скорости колеса к угловой скорости его вращения rk = vx /wk.
В соответствии с принятым выше определением, уменьшение пути центра колеса за определенное число его оборотов равносильно уменьшению радиуса качения.
Если направление передаваемого момента будет противоположным направлению угловой скорости вращения колеса (тормозящее колесо), при увеличении момента радиус качения будет возрастать.
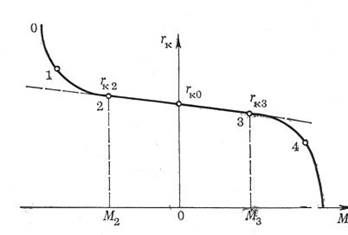
Рис. 3.6. Зависимость радиуса качения колеса от передаваемого ему крутящего момента
Зависимость радиуса качения колеса от передаваемого ему крутящего момента показана на рис. 3.6. На участке 2—3 радиус качения линейно зависит от передаваемого момента, и его изменение определяется упругим проскальзыванием колеса. Акад. Е. А. Чудаковым, впервые установившим эту зависимость, предложена следующая формула для нахождения радиуса качения по передаваемому колесу моменту:
rk=rk0—ltMk
где rk0 — радиус качения при нулевом крутящем моменте, который соответствует радиусу качения колеса в ведомом режиме;
lt — коэффициент тангенциальной эластичности шины, зависящий от типа и конструкции шины.
На участках 1—2 и 3—4 изменение радиуса качения определяется как упругим проскальзыванием, так и скольжением колеса. Пунктирной линией на графике показано, как изменялся бы радиус качения при отсутствии скольжения. Очевидно, что на участках 1—2 и 3—4 он может находиться также по формуле (1.2). В последующем радиус качения, определенный при отсутствии скольжения, будем называть радиусом качения без скольжения и обозначать r0.
На участках 0—1 и 4—5 происходит полное скольжение элементов шины относительно опорной поверхности. Точка 5 соответствует буксующему колесу при неподвижном автомобиле, а точка 0—колесу, движущемуся юзом.
Если обозначить радиусы качения и передаваемые колесом моменты в начале и в конце линейного участка соответственно через М2, rк2 и М3, rк3, то коэффициент тангенциальной эластичности шины определим как
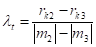
Экспериментально радиус качения находят путем определения числа оборотов колеса N на отрезке пути s при заданном режиме движения:
rk=s/(2pN).
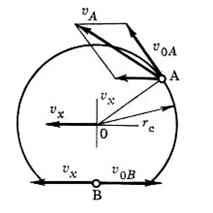
Рис. 3.7.
Согласно рис. 3.7, скорость точки В (скорость vs) можно рассматривать как скорость скольжения элементов шины относительно опорной поверхности. В соответствии с принятыми обозначениями
vs = vx — voB=wк(rк—rо).
Отсюда следует, что при rк=rо колесо катится без скольжения. Если rк>rо, скорость скольжения положительна и ее направление совпадает с направлением поступательной скорости колеса (колесо движется юзом). При rк<rо скорость скольжения отрицательна и направлена в сторону, противоположную вектору поступательной скорости центра колеса (колесо движется с буксованием).
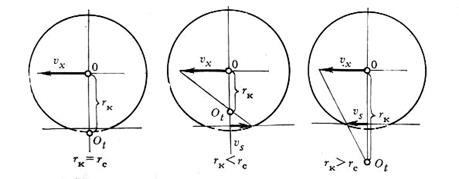
Рис. 3.8. Положения мгновенных центров вращения колеса
На рис. 3.8 показаны планы скоростей для рассмотренных трех случаев качения колеса. Из рисунка следует, что радиус качения является расстоянием от центра колеса до его мгновенного центра вращения Оt и в зависимости от режима движения может изменяться от нуля (буксующее колесо при неподвижном автомобиле) до бесконечности (заблокированное колесо при движущемся автомобиле).
3.3. Момент сопротивления качению эластичного колеса в ведомом режиме
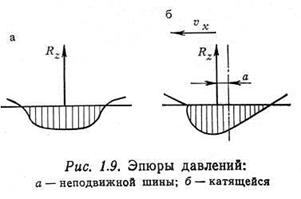
Шина деформируется под действием нормальной к опорной поверхности составляющей нагрузки на колесо. Площадь контакта ее с дорогой увеличивается до тех пор, пока не наступит равновесие между нормальной реакцией дороги и нагрузкой. У неподвижной шины контактная поверхность имеет форму, близкую к эллипсу, большая ось которого находится в плоскости симметрии шины. Распределение давления по площади контактной поверхности неравномерное, оно примерно пропорционально деформации шины. Характерная эпюра давлений под неподвижной шиной показана на рис. 3.9, а.
Рис. 3.9. Эпюры давлений: о—неподвижной шины; б—катящейся. |
Рис. 3.10. Деформация элементов шины при качении |
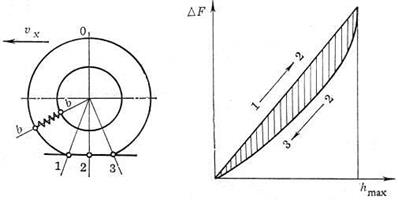
При движении автомобильного колеса в работе участвуют все элементы шины. За один оборот колеса каждый элемент профиля шины, например элемент b—b (рис. 3.10, а), подвергается полному циклу нагружения и разгрузки.
С достаточной для практической цели точностью можно считать, что нагружение (деформирование) элементов шины происходит в зоне полуокружности 0—1—2, а восстановление формы — полуокружности 2—3—0. При этом наиболее интенсивное деформирование и восстановление происходят в зонах полудуг 1—2 и 2—3 соответственно.
По мере перемещения элемента шины от точки 1 к точке 2 увеличивается его деформация и, следовательно, воспринимаемая им нагрузка. Зависимость нагрузки DF, передающейся на элемент, от его деформации представлена на графике рис. 3.10, б (линия 1—2). При перемещении элемента от точки 2 к точке 3 происходит уменьшение деформации (уменьшение нагрузки, приходящейся на элемент). На графике линия, характеризующая зависимость DF=f(h) вследствие неизбежных гистерезисных потерь пройдет ниже линии, показывающей ту же зависимость при увеличении деформации (линия 2—3). Площадь, заключенная между линиями нагружения и разгрузки, пропорциональна потерям энергии на деформацию элемента шины при одном обороте колеса.
Вследствие того, что при одинаковых прогибах в зонах увеличения и уменьшения деформации на элементы шины приходится разная нагрузка, эпюра давлений для катящегося колеса оказывается несимметричной относительно середины контактной поверхности: в передней части контактной поверхности нормальные давления будут большими, нежели в задней. Поэтому равнодействующая нормальных реакций смещена на расстояние а от середины контактной поверхности (см. рис. 3.9, б). За счет этого смещения создается момент относительно оси колеса
Mf=aRz,
где Rz — нормальная к опорной поверхности составляющая реакции дороги.
Этот момент препятствует качению колеса. Поэтому его можно считать моментом сопротивления качению колеса. Отметим, что на недеформируемой поверхности момент сопротивления качению обусловлен внутренними (гистерезисными) потерями энергии на деформацию шины.
В дальнейшем вместо момента сопротивления качения колеса мы будем рассматривать силу сопротивления качению колеса Ff=Mf / r0=aRz/ r0= fRz.
Здесь f=a/r0 – коэффициент сопротивления качению колеса. Коэффициент сопротивления качению колеса характеризует потери энергии, возникающие при качении колеса.
3.4. Влияние конструктивных и эксплутационных факторов на коэффициент сопротивления качению.
На коэффициент сопротивления качению влияют:
1. тип покрытия дороги и ее состояние;
2. скорость движения;
3. давление воздуха в шинах;
4. температура шины;
5. нагрузка на колесо;
6. его размеры;
7. конструктивные особенности шины.
Увеличение скорости движения. Как правило, коэффициент f при увеличении v возрастает. На ровных дорогах при изменении скорости от нуля до некоторого значения, зависящего от конструктивных особенностей шины, нормальной нагрузки на колесо и внутреннего давления воздуха, возрастание коэффициента f невелико. Поэтому для большинства шин грузовых автомобилей связь коэффициента f и скорости v достаточно точно аппроксимируется линейной зависимостью. На неровных дорогах даже при средних скоростях с увеличением v коэффициент f может расти довольно сильно. Начиная с некоторого значения v даже на ровных дорогах коэффициент f начинает быстро увеличиваться (рис. 3.11).
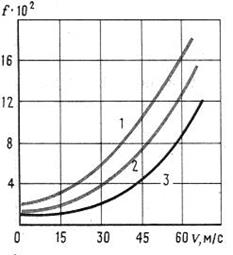
Рис.3.11. Зависимость коэффициента сопротивления качению при различных значениях рВ: 1-3 соответственно 15, 25 и 30 МПа
При номинальных нагрузках на колесо и давлениях воздуха в шине интенсивный рост коэффициента f начинается при v=20…30 м/с.
Существуют различные эмпирические формулы, позволяющие приближенно подсчитать коэффициент f при различных скоростях движения; удобной является формула
f=f0+kfv2,
где f0 — коэффициент сопротивления качению при малой скорости. В тех случаях, когда действительное значение kf неизвестно, рекомендуется принимать kf=7×10-6
Температура шины. С увеличением температуры шины ее сопротивление качению снижается, во-первых, за счет уменьшения гистерезисных потерь в резине, во-вторых, в результате повышения внутреннего давления воздуха.
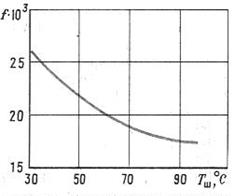
Рис. 3.12. Зависимость коэффициента сопротивления качению от температуры шины
При этом снижается коэффициент f в результате уменьшения деформаций шины (рис. 3.12). Приводимые в литературе значения f относятся обычно к полностью прогретой шине.
Давление воздуха в шине рв. Коэффициент f на различных дорогах в различной степени зависит от рв. На дорогах с твердым покрытием он уменьшается с увеличением давления рв, достигая минимального значения при давлении рв, близком к рекомендованному для данной шины. При чрезмерном давлении рв возрастают динамические нагрузки, возникающие в результате взаимодействия колеса с неровностями дороги, что может привести к некоторому возрастанию коэффициента f.
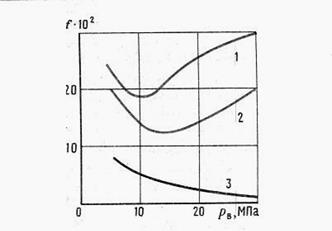
Рис. 3.13. Зависимость коэффициента сопротивления качению от внутреннего давления воздуха в шине на разных поверхностях: 1- песок; 2- пашня; 3- асфальт
Если движение происходит по деформируемым дорогам, при уменьшении давления рв увеличиваются потери, связанные с деформацией шины, но уменьшаются потери, связанные с деформацией дороги. Можно подобрать такое давление рв.опт, при котором сопротивление качению будет минимальным (рис. 3.13). Оптимальное давление тем меньше, чем больше деформируемость дорожного полотна. Такая зависимость коэффициента сопротивления качению используется для повышения проходимости автомобилей с центральной системой регулирования давления в шинах.
Нагрузка на колесо Рz. При неизменном давлении рв увеличение Рz приводит к возрастанию коэффициента f. На дорогах с твердым покрытием при изменении нагрузки в пределах 80…110 % номинальной увеличение коэффициента f несущественно. При превышении нагрузки на 20 % номинального значения коэффициент возрастает приблизительно на 5 %, а при дальнейшей перегрузке — более интенсивно. Сильно возрастает коэффициент f с увеличением нагрузки Рz на деформируемой опорной поверхности.
Конструктивные параметры шины. Значение коэффициента f зависит от большого числа конструктивных параметров.
Увеличение толщины протектора повышает коэффициент f, особенно у диагональных шин. В связи с этим по мере износа шин сопротивление качению падает. При полностью изношенном протекторе сопротивление качению может уменьшиться на 20…25 % по сравнению с неизношенным. У шин с вездеходным рисунком протектора, имеющих толщину протектора почти в 2 раза большую, чем у шины с дорожным рисунком, при качении по дорогам с твердым покрытием коэффициент f на 25…30 % больше.
Уменьшение отношения высоты Н профиля шины к его ширине В приводит к снижению коэффициента сопротивления качению. Снижение Н/В уменьшает также зависимость коэффициента f от скорости движения.
Внутреннее строение каркаса шины оказывает существенное влияние на коэффициент сопротивления качению. При v<30… 35 м/с наименьшим сопротивлением качению обладают радиальные шины (коэффициент f у них меньше, чем у диагональных на 15…20 %). При больших скоростях наименьшим коэффициентом обладают диагонально-опоясанные и низкопрофильные диагональные шины. По мере износа преимущество радиальных шин по сравнению с диагональными уменьшается.
Увеличение диаметра колеса приводит к уменьшению коэффициента f. На ровных дорогах с твердым покрытием уменьшение небольшое. Чем больше размеры и число неровностей на дороге и чем больше на таких дорогах скорость движения, тем значительнее влияние диаметра колеса на коэффициент f. Особенно сильно снижается коэффициент f на деформируемых опорных поверхностях.
Увеличение ширины колеса на дорогах с твердым покрытием незначительно увеличивает коэффициент f, а на большинстве деформируемых опорных поверхностях существенно снижает.
Совершенствование качества резины позволяет значительно снизить сопротивление качению.
На автомобилях со сдвоенными колесами (грузовые автомобили, автопоезда и др.) дополнительные потери на качение возникают также в результате неравномерного распределения между шинами сдвоенных колес нормальных нагрузок и крутящих моментов. Причиной неравномерности являются неодинаковые геометрические размеры и износ шин, различие в температуре, наличие поперечного уклона дороги, прогиб балки моста, неодинаковость внутреннего давления воздуха и др. Вся совокупность конструктивных мероприятий, улучшающих энергетические свойства шин, позволяет снизить их сопротивление качению в 2…3 раза.
studizba.com
Парадокс колеса — Мастерок.жж.рф — LiveJournal
Впервые о парадоксе колеса заговорили ещё до Аристотеля, однако он первый вплотную занялся его изучением. Затем над решением этой задачки бился Галилео Галилей. Хотя многим это покажется совершенно очевидным. Но давайте по порядку …
Аристотелево колесо — так называют обыкновенно кажущийся парадокс, представляющийся при движении колеса около оси, когда самое колесо катится на плоскости по прямой линии. Полагают, что Аристотель впервые заметил этот странный парадокс, который по этой причине и удержал наименование «Аристотелева колеса».
Положим, что круг, обращаясь вокруг своего центра, катится в то же время по прямой линии и с совершением полного оборота описывает прямую, коей длина равна окружности круга. Если в этом круге, который назовем главным, вообразим другой, меньший, одноцентренный с первым и движущийся вместе с ним, то по совершении большим кругом полного оборота малый круг опишет прямую линию, равную уже не своей окружности, а окружности главного круга. Пример подобного кажущегося парадокса можно видеть в движении каретного колеса, ступица которого при своем обращении перейдет прямую, большую своей окружности и равную окружности самого колеса. Приведенный пример, как известно, подтверждается ежедневным опытом.
Но тут рождается вопрос, как объяснить, что окружность ступицы описывает прямую, большую этой самой распрямленной окружности?
А если представить, что всё это правда? Тогда технически возможно, что колесо с окружностью в 2,54 сантиметра в состоянии пройти тот же путь за один оборот, что и колесо с окружностью, равной 1,6 километров.
Но такого просто не бывает. Длина окружности с меньшим радиусом не может быть равна длине окружности с большим радиусом. Так в чём же дело?

Решение Аристотелем данного парадокса заключается в ясном и последовательном изложении всех моментов факта, представляющего некоторое затруднение. Галилей, также пытавшийся объяснить приведенный парадокс, вообразил бесчисленное множество бесконечно малых пустот (vuldes infiniment petits), распределенных по двум прямым линиям, описываемым обоими кругами; он утверждал, что малый круг не касается точками своей окружности к пустым пространствам переходимой им прямой линии и, таким образом, описывает только линию, равную длине своей окружности. Нет надобности, кажется, доказывать слишком очевидную неосновательность подобного объяснения. Существуют и другие попытки ученых объяснить явление так называемого Ар. колеса, но все они большею частью неудовлетворительны.
Первое настоящее решение этого парадокса было предложено членом Парижской академии Дорту-де-Мераном (Dortous de Mairan) в 1715 г. Он объяснил кажущееся противоречие приведенного случаяскольжением ступицы колеса по прямой линии, переходимой точками ее окружности.
Можно разрешить затруднение еще и другим образом. Вообразим круг, обращающийся около своего центра в то время, как последний (т. е. центр) движется по прямой линии; очевидно, что прямолинейное движение центра вовсе не зависит от вращательного движения круга, а следовательно, и отношение скоростей, соответствующих обоим движениям, вполне произвольно. Очевидно, что легко уподобить катящееся на плоскости колесо с кругом, обращающимся около своего центра, между тем как этот центр движется параллельно упомянутой плоскости. Следовательно, так же легко вообразить движение колеса, как и движение круга.
Давайте проследим маршрут, который проходит каждая точка окружности от начала красной линии до её конца. Перемещайте свой палец по линии, обозначающей радиус круга, одновременно следя за траекторией, которую проходит малая окружность от начала пути до конца.
Затем проследите траекторию, которую проходит большая окружность от начала пути до конца. Очевидно, что точка на большей окружности проходит бо́льшую траекторию, а, следовательно, больший путь, чтобы добраться до той же точки.
Иначе говоря, можно ехать в Москву из Нижнего Новгорода через Владимир, а можно через Архангельск или Астрахань. Расстояние от Нижнего до Москвы остаётся неизменным, но пути, которые придётся проделать по этим маршрутам, далеко не одинаковы.
Можно это объяснить еще вот так: этот парадокс возник из-за непонимания разницы между словами «путь» и «перемещение». Перемещение будет одинаково в любом случае ( если вы переместите камень на километр при любом радиусе любая его точка переместится на километр) а вот путь они проходят разный, путь это то расстояние которое прошли точки пересечения линии, которая отсекает полный оборот, с окружностями и он разный)
В этом-то и заключается объяснение парадокса, над которым ломали голову самые выдающиеся умы человечества.
[источники]
источники
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон. 1890—1907.
http://io9.com/the-wheel-paradox-that-stumped-aristotle-and-galileo-1507994415
Почитайте еще про Парадокс Монти Холла и действительно ли Великая теорема Ферма доказана ?. Давайте еще вспомним про Тест куклы Кларка Оригинал статьи находится на сайте ИнфоГлаз.рф Ссылка на статью, с которой сделана эта копия — http://infoglaz.ru/?p=42386
masterok.livejournal.com
Kvant. Плоскопараллельное движение — PhysBook
Фистуль М. Кинематика плоскопараллельного движения //Квант. — 1990. — № 9. — С. 42-44.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Что общего между вращением Земли вокруг своей оси, движением стрелок часов, колес автомобиля на прямолинейном участке пути и т. п.? С точки зрения кинематики, все это примеры так называемого плоскопараллельного движения твердого тела, при котором все точки тела перемещаются в параллельных плоскостях.
Разумеется, в самом общем случае различные точки тела могут двигаться по-разному. Однако принято выделять два частных случая и говорить о двух простейших типах движения — о поступательном движении и о вращении вокруг неподвижной оси. В первом случае все точки тела совершают одинаковые перемещения. Это движение самое простое, и здесь мы его обсуждать не будем. Во втором случае все точки описывают одинаковые траектории — окружности с центрами на оси вращения. Основной характеристикой такого движения является угловая скорость вращения ω.
Давайте вычислим, например, угловые скорости стрелок часов. Так как стрелки вращаются равномерно, то угол поворота φ со временем изменяется по закону φ = ωt (уравнение равномерного вращения). Секундная стрелка делает один оборот за 60 секунд; следовательно, ее угловая скорость равна ωс = 2π / 60 с = 0,1047 с-1. Аналогично, скорость часовой стрелки равна ωч = 2π / (12·60·60) с = 0,0001455 с-1.
Рис. 1
А как добиться того, чтобы секундная и часовая стрелки двигались с различными угловыми скоростями, но синхронно? Оказывается, для этого используется зубчатая передача: два зубчатых колеса могут вращаться вокруг разных осей, но при этом они входят в зацепление друг с другом (рис. 1). Поскольку линейные скорости точки А одинаковы —
\(~\upsilon_A = \omega_1 R = \omega_2 r\) ,получаем
\(~\frac{\omega_1}{\omega_2} = \frac{r}{R} = \frac{z_1}{z_2}\) ,где z1 и z2 — число зубцов шестеренок.
Кроме того, можно заметить, что при внутреннем зацеплении вращение шестеренок происходит в одном направлении, а при внешнем — в противоположных направлениях. С помощью таких (и более сложных) зубчатых передач осуществляется соединение стрелок в часах, передача усилий в домкрате, изменение величины скорости и «задний ход» у автомобиля.
Теперь рассмотрим более сложное плоскопараллельное движение твердого тела, когда тело вращается, но ось вращения сама поступательно перемещается в пространстве. Скорости такого движения проще всего найти, используя понятие мгновенного центра вращения — так называют точку, скорость которой в данный момент времени равна нулю. Скорости всех остальных точек тела при этом будут такими, как будто тело вращается вокруг неподвижной оси, проходящей через мгновенный центр вращения.
Рис. 2
В качестве примера разберем движение колеса на прямолинейном участке пути без проскальзывания. Так как колесо не проскальзывает, точка С (рис. 2), в которой колесо касается дороги, имеет скорость равную нулю. Значит, точка С и есть мгновенный центр вращения. Найдем, какой будет угловая скорость вращения колеса, если скорость его центра О (скорость поступательного движения колеса) равна υ0:
\(~\upsilon_0 = \omega r\) , и \(~\omega = {\upsilon_0}{r}\) .Легко находится и скорость произвольной точки А. Она направлена по линии АВ и равна
\(~\upsilon_A = \omega \cdot CA = 2 \omega r \cos \alpha = 2 \upsilon_0 \cos \alpha\) .На рисунке 2 изображена также траектория, которую описывает каждая точка обода катящегося колеса. Эта удивительная кривая — циклоида — встретится вам во многих случаях: по такой траектории движутся частицы в «скрещенных» (взаимно перпендикулярных) электрическом и магнитном полях, по циклоиде шарик скатывается за минимальное время и т. д.
Теперь легко ответить на вопрос, который обычно вызывает затруднения: почему, если смотреть на движущегося велосипедиста, то верхние спицы колес сливаются в одно целое, а нижние видны раздельно. Очевидно, это связано с тем, что скорости нижней половины колеса меньше, чем верхней (подумайте, почему, если смотреть на велосипедиста из окна движущегося в ту же сторону автобуса, этот эффект пропадает?).
Рис. 3
А что если мы захотим определить скорость колес вагона движущегося поезда? Мы обнаружим, что на ободе колеса имеются точки, которые движутся назад, в противоположную движению поезда сторону. Это — точки выступающей части колеса, например точка А на рисунке 3. Мгновенный центр вращения (точка С) находится на неподвижном рельсе, по которому колесо катится без проскальзывания. Траектория точки обода колеса еще более любопытна, чем в предыдущем случае,— на траектории имеются возвратные участки движения (петли). Интересно отметить, что аналогичные петлеобразные траектории описывают в своем движении планеты. Их наблюдали еще древнегреческие астрономы, однако объяснить увиденное они не смогли. Сейчас мы знаем, что эти траектории связаны с наложением двух вращений — Земли и наблюдаемой планеты вокруг Солнца.
Всегда ли при плоскопараллельном движении траектории оказываются такими сложными? Попробуйте определить, например, какую траекторию описывают точки обода колеса радиусом r, которое катится по внутренней поверхности неподвижного колеса радиусом 2r.
Рис. 4
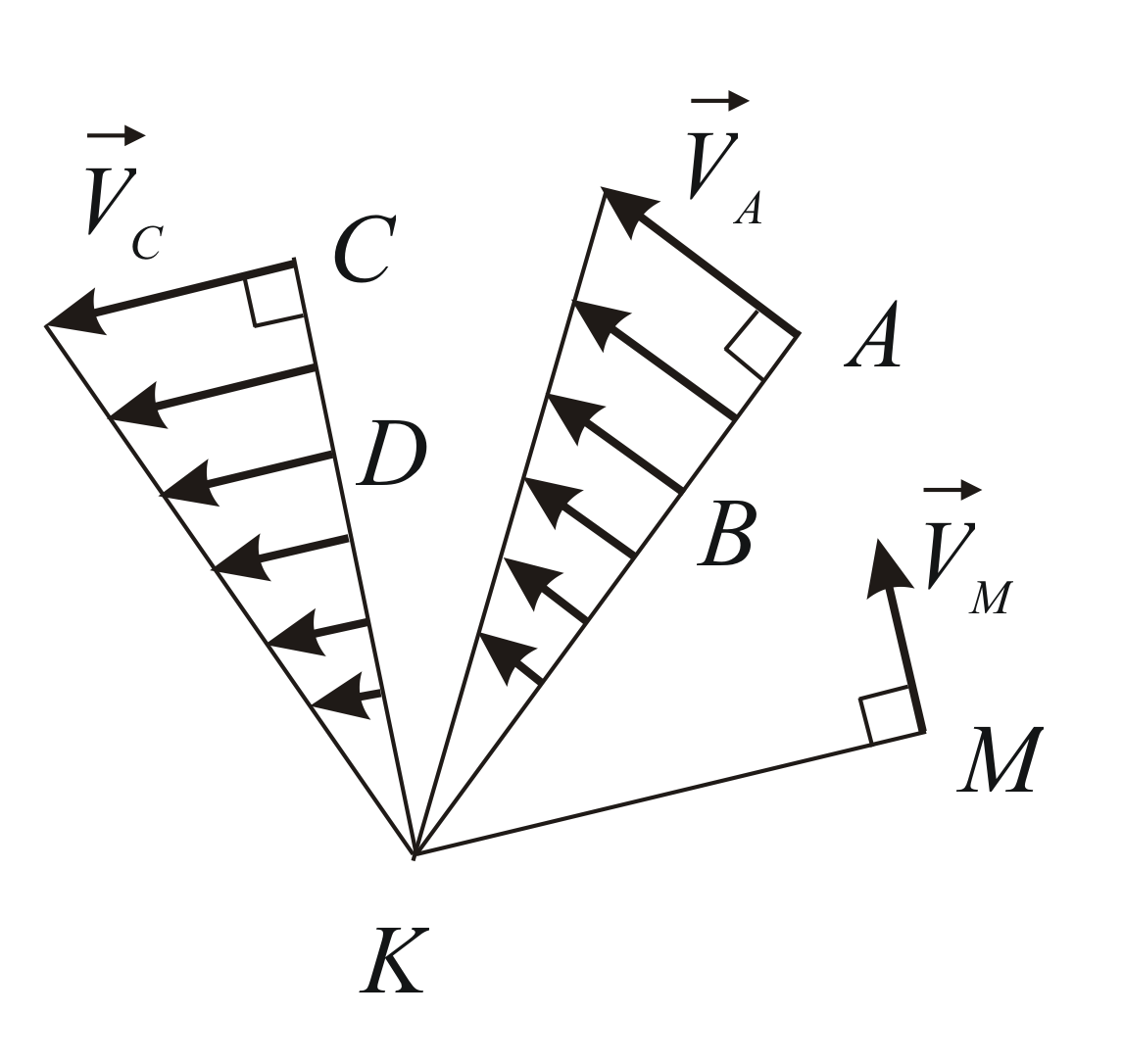
В заключение мы хотим познакомить вас с простым по конструкции, но важным для практики прибором — линейкой-эллипсографом (рис. 4), который служит для вычерчивания эллипсов. Точки А и В такого прибора двигаются по взаимно перпендикулярным направляющим ОА и OB, a точка М при этом описывает эллипс (подумайте, почему). Где находится мгновенный центр вращения в этом случае? Как найти скорость точки М, зная скорости точек А и В?
Рассмотрим жесткий треугольник СВА (точка С лежит на пересечении перпендикуляров к направляющим). Проекции скоростей двух точек твердого тела на линию их соединения всегда равны. Для точек С, А и С, В это возможно, если υC, т. е. если точка С — мгновенный центр вращения. Скорость точки М можно определить, зная скорость точки А, например:
\(~\upsilon_A = \omega \cdot CA\) , и \(~\upsilon_M = \upsilon_A \cdot \frac{CM}{CA}\) .Аналогичным образом, используя понятие мгновенного центра вращения, можно легко находить скорости любых точек механизмов, совершающих плоскопараллельное движение.
www.physbook.ru