Передаточное число это отношение: «Что такое передаточное число, и как оно влияет на работу механизма?» – Яндекс.Кью

alexxlabОпубликовано

Содержание

«Что такое передаточное число, и как оно влияет на работу механизма?» – Яндекс.Кью

В отличие от других ответчиков я начну с интеграла, а не с производной. Интеграл в жизни имеет конкретный физический смысл. Это площадь фигуры ограниченной осью абцисс Х и графиком функции. Далеко от жизни? Сейчас приблизим. Представим себе машину, которая едет. Отложим по оси Х время в пути, а по Y — скорость в каждый, конкретный момент времени, и начертим график скорости от времени. Если скорость постоянная — это будет горизонтальная прямая. Фигура ограниченная этой прямой и осью Х — будет прямоугольником. Ширина прямоугольника — время в пути, а высота — скорость машины. Ширина*высота=площадь. Но при этом время*скорость=расстояние. Т.е. расстояние равно площади! И пройденное расстояние — это интеграл скорости.

А теперь начинается магия математики. Как посчитать путь, который пройдет машина, если у неё непрерывно меняется скорость, и её график извилистая кривая? А очень просто. Ведь ничего не изменилось — надо только найти площадь фигуры на графике! Как мы будем искать эту площадь — не важно. Можно просто посчитать клеточки на бумаге (это будет численным интегрированием, которое всегда приблизительное). А если скорость описана функцией от времени — можно найти её интеграл и сразу получить точный ответ.

А диференцирование — это это действие обратное интегрированию. Если продиференцировать функцию расстояния от времени, которую получили интегрированием скорости — мы обратно получим скорость. Ту самую скорость, с которой меняется пройденный путь машины. Сейчас скорость большая, километровые столбы мелькают, и пройденный путь быстро растет, а когда скорость падает и пройденные километры набираются медленно. На графике пути от времени, скорость это наклон самого графика. Грфик идет вверх — скорость положительная, мы едем вперед и расстояние растет. График пошел вниз — скорость отрицательная, мы едем обратно, а расстояние до точки старта уменьшается. График горизонтальная линия (наклона нет) -скорость равна нулю, мы стоим и расстояние неизменно.

Немного решил дописать.

Вообще интеграл в изменяющихся физических процессах очень востребован. А любой процесс описывает какую-то жизненную ситуацию.

Это сколько воды натекло через трубу в пресловутый бассейн при переменном напоре. Сколько киловатт накрутил электросчетчик при переменной нагрузке на сеть. До какой температуры нагрелась вода в кастрюле, если в процессе нагрева мы регулировали мощность плиты.

Любой процесс изменяемый во времени можно интегрировать и получить полезный результат. То же касается и дифенциала, который показывает скорость изменения общего результата.

Передаточное отношение и передаточное число

Автор admin На чтение 6 мин. Просмотров 284

Незаменимыми помощниками человека в любой его деятельности являются механизмы. Но сам по себе механизм – просто набор деталей. Для того чтобы он работал, его надо обеспечить энергией. Ее подают от отдельного устройства – двигателя или силовой установки при помощи специальных механизмов, называемых передачами. Так уж сложилось исторически – в технике чаще всего используется вращательное движение, хотя применяются и другие виды. При процессе перехода энергии она может меняться, это изменение происходит в соответствии с тем, какое передаточное отношение имеет механизм.

О том, что при этом происходит

Самый простой пример передачи – от вращающегося колеса водяной мельницы к жернову. При этом зачастую происходит изменение первоначальной энергии, полученной колесом от текущей воды, по величине и направлению. Величину такого изменения будет определять передаточное отношение. Оно описывает одну из важнейших характеристик преобразования энергии при вращательном движении, определяемую как отношение частоты или скорости вращения элемента, получающего энергию, к тем же параметрам элемента, отдающего энергию.

передаточное отношение редукторапередаточное отношение редуктора
Иными словами, передаточное отношение описывает, как изменяется исходная энергия, получаемая от двигателя или любого другого источника энергии (водяного, ветряного колеса, турбины и т.д.), при ее передаче.
За всю историю развития техники человечество создало самые разнообразные передачи, для каждой из которых существует передаточное число, являющимся частным от деления скорости ведущего звена на скорость ведомого.

Передаточное отношение ременной передачи

Ременной передачей называют два шкива, которые соединяет ремень, как это показано на рисунке. Возможно, что она была одним из первых способов, которые применял человек. Менялся материал, используемый для изготовления ремня, менялась его форма, но неизменным оставалось передаточное отношение, определяемое как частое от деления скорости ведущего вала, на скорость ведомого, или как результат деления числа оборотов этих валов (n1/n2 или ω1/ω2).

Для ременной передачи оно может быть рассчитано с использованием диаметров (радиусов) шкивов. Передаточное число в таком случае также определяется как частное от деления оборотов.

Если при преобразовании энергии число оборотов понижается, то есть передаточное число больше 1, то передача будет понижающей, а само устройство носит название редуктора. Если результат меньше единицы, то устройство называется мультипликатором, хотя оно также выполняет функции редуктора, только понижающего. Передаточное отношение редуктора позволяет уменьшить число оборотов (угловую скорость), поступающих с ведущего вала на ведомый, увеличив при этом передаваемый момент.

Это свойство редуктора дает возможность добиваться инженерам при проектировании различных устройств изменения параметров передаваемой энергии, а передаточное отношение редуктора служит при этом мощным инструментом в решении поставленной задачи.

Несмотря на значительный возраст, для ременной передачи и сейчас находится работа на автомобиле, она используется как привод генератора, газораспределительного механизма, а также в некоторых других случаях.
передаточное отношение ременной передачи

передаточное отношение ременной передачи

Передаточное отношение цепной передачи

В подобной ременной передаче ремень может быть заменен на цепь, в этом случае шкивы также должны быть заменены на звездочки. Полученная передача называется цепной, она знакома каждому, ведь именно такая применяется на велосипедах. Для нее передаточное отношение определяется так же, как для ременной, но можно воспользоваться и соотношением количества зубьев на звездочках (ведущей и ведомой). Однако при таком расчёте передаточное отношение будет обратным, то есть передаточное число определяется делением числа зубьев ведомой звездочки на число зубьев ведущей (z2/z1).

цепная передачацепная передача
Отличительной особенностью цепной передачи является повышенный уровень шума, а также износ при работе на высоких скоростях, поэтому ее при необходимости использования лучше всего ставить после уменьшения оборотов. В автомобиле возможно применение цепной передачи для привода ГРМ, правда, ограничением такого применения является повышенный уровень шума при ее работе.

Передаточное отношение зубчатой передачи

Так называется механизм, в котором используются колеса с зубьями, находящимися в зацеплении. Она считается наиболее рациональной и востребованной для машиностроения. Существует множество разнообразных вариантов изготовления подобных колес, отличающихся по расположению осей, форме зубьев, способу их зацепления и т.д. Как в случае с цепной, для зубчатой передаточное число определяется делением числа зубьев шестерен (z2/z1).

Многообразие вариантов построения зубчатой передачи предоставляет возможность использовать их в разных условиях, от тихоходного редуктора до высокоточных приводов.
зубчатая передача

зубчатая передача
Для зубчатой передачи характерны:

  • постоянное передаточное число;
  • компактность;
  • высокий кпд;
  • надежность.

Одной из разновидностей зубчатой передачи считается червячная. Она используется в тех случаях, когда передача момента осуществляется между скрещивающимися валами, для чего применяется такой элемент как червяк, представляющий собой винт специальной конструкции с резьбой. Для определения передаточного отношения червячной передачи выполняют деление количества зубьев колеса (червячного) z2 на число заходов резьбы червяка z1.

Планетарная передача

Этот вид зубчатой передачи, содержащей колеса с геометрическими осями, имеющими возможность перемещения. Что она собой представляет, можно понять из приведенного ниже рисунка. По сути дела, это уже конструкция своеобразного планетарного редуктора, включающего в свой состав некоторое число шестерен, взаимодействующих между собой. У каждой из них свое название – солнце, корона, сателлит.

Для такого планетарного редуктора изменение момента зависит от того, какая из его шестерен неподвижна, на какую подан крутящий момент, и с какой он снимается.
устройство планетарного редуктора

устройство планетарного редуктора
При любом использовании планетарного редуктора, один из трех его элементов будет неподвижен. У такого, планетарного варианта построения передач, по отношению к простой зубчатой или ременной, есть возможность получить существенное изменение момента при небольшом количестве колес и габаритах устройства. В автомобиле у подобного планетарного устройства своя сфера применения – в составе АКПП, а также в гибридных транспортных средствах, для обеспечения совместной работы ДВС и электромотора. Широкое применение планетарного редуктора осуществляется в гусеничной технике.

О главной паре

Практически все виды передач используются в автомобиле – крутящий момент от двигателя проходит цепочку различных устройств и претерпевает изменения, начиная от КПП, главной пары, и заканчивая колесами автомобиля. Все передаточные отношения для КПП и главной пары влияют непосредственным образом на динамику автомобиля.
Поэтому с целью

  1. уменьшения частоты переключения;
  2. возможности движения при спокойной езде на небольших оборотах двигателя;
  3. повышения верхнего порога скорости движения,

передаточные отношения, в том числе и для главной пары, должны быть уменьшены. Для улучшения разгонной динамики все должно быть наоборот.

Работа различных механизмов и устройств, в том числе и в автомобиле, не может происходить без преобразования используемой энергии, как по величине, так и по направлению. Оценить и рассчитать величину необходимого изменения, а также его последствия, помогает передаточное отношение.

Мне нравится1Не нравится

Передаточное отношение — Википедия

Передаточное отношение ( i {\displaystyle i} ) — одна из важных характеристик механической передачи вращательного движения. Передаточное отношение показывает,

во сколько раз вырос момент силы на ведомом валу по сравнению с ведущим.

i = i 12 = d 2 d 1 = z 2 z 1 = M 2 M 1 = ω 1 ω 2 = n 1 n 2 {\displaystyle i=i_{12}={\frac {d_{2}}{d_{1}}}={\frac {z_{2}}{z_{1}}}={\frac {M_{2}}{M_{1}}}={\frac {\omega _{1}}{\omega _{2}}}={\frac {n_{1}}{n_{2}}}}

где: i 12 {\displaystyle i_{12}}  — передаточное отношение от звена 1 к звену 2 (звено 1 — ведущее, звено 2 — ведомое)

d 1 , d 2 {\displaystyle d_{1},d_{2}}  — диаметры звеньев

z 1 , z 2 {\displaystyle z_{1},z_{2}}  — количество зубьев звеньев (если таковые имеются)

M 1 , M 2 {\displaystyle M_{1},M_{2}} — крутящие моменты звеньев

ω 1 , ω 2 {\displaystyle \omega _{1},\omega _{2}}  — угловые скорости звеньев

n 1 , n 2 {\displaystyle n_{1},n_{2}}  — частоты вращения звеньев

Таким образом, если передаточное отношение больше единицы, то передача увеличивает момент силы на ведомом валу, но понижает угловую скорость и частоту.

Поэтому редуктор с передаточным отношением больше единицы называется понижающим.

Размышляя о моменте силы, становится понятным следующее соотношение для многоступенчатых передач:

i = i 14 = i 12 ⋅ i 23 ⋅ i 34 = M 2 M 1 ⋅ M 3 M 2 ⋅ M 4 M 3 = M 4 M 1 {\displaystyle i=i_{14}=i_{12}\cdot i_{23}\cdot i_{34}={\frac {M_{2}}{M_{1}}}\cdot {\frac {M_{3}}{M_{2}}}\cdot {\frac {M_{4}}{M_{3}}}={\frac {M_{4}}{M_{1}}}}

Однако следует учесть, что данное выражение истинно только в случае отсутствия потерь в зацеплении и других подвижных частях механизма на трение, упругие деформации и другие факторы, что в принципе является невозможным. Поэтому при конструкторских расчетах силовых и кинематических параметров машин необходимо учитывать коэффициент полезного действия как непосредственно самой передачи, так и пар подшипников, а если они есть, то и соединительных муфт. С учетом этого общая формула для определения момента на выходном валу имеет вид [4, с. 12]:

i i , i + 1 ⋅ M i ⋅ η = M i + 1 , {\displaystyle i_{i,i+1}\cdot M_{i}\cdot \eta =M_{i+1},}

где i i , i + 1 {\displaystyle i_{i,i+1}}  — передаточное отношение механизма;

M i , M i + 1 {\displaystyle M_{i},M_{i+1}}  — крутящие моменты на входном и выходном валах механизма соответственно;

η {\displaystyle \eta }  — КПД механизма.

Следующий абзац возник из-за некоторого разногласия в рядах студентов по поводу ведущего и ведомого звена.

Из курсового проектирования деталей машин [5, с. 118]: «Как правило ременная и цепная передачи служат для понижения частоты вращения. Специальные передачи, повышающие угловую скорость, здесь не рассматриваются, так как в типовых заданиях на курсовое проектирование они не встречаются.»

В этой же книге [4, с. 7] дана формула i = n n o m n p {\displaystyle i={\frac {n_{nom}}{n_{p}}}} . Здесь в качестве номинальной n n o m {\displaystyle n_{nom}} частоты принимается частота работы электропривода (то есть ведущего звена), а в качестве расчетной n p {\displaystyle n_{p}}  — частота ведомого звена. Также даны средние значения для различного рода передач: зубчатых 2-6, червячных 8-80, цепных 3-6, ременных 2-4. То есть скорость ведущего звена в i {\displaystyle i} раз больше чем скорость ведомого звена.

Проверка: редуктор, передаточное число которого больше единицы (2>1), скорость понижается (n2<n1), i = ω 1 ω 2 = n 1 n 2 = 2   m / c 1   m / c = 2 {\displaystyle i={\frac {\omega _{1}}{\omega _{2}}}={\frac {n_{1}}{n_{2}}}={\frac {2~m/c}{1~m/c}}=2} . (Момент силы увеличивается)

В случае зубчатых шестерён передаточное отношение всегда является рациональным числом. Характеристика передаточное отношение применима как к механической передаче с одной ступенью (одной кинематической парой), так и к механическим передачам со множеством ступеней. Во втором случае передаточное отношение всей механической передачи будет равно произведению передаточных отношений всех ступеней.

Формально механизмы с передаточным отношением больше единицы называются редукторами, с передаточным отношением меньше единицы — мультипликаторами. Фактически и тот, и другой механизм в обиходе можно называть редуктором, добавляя лишь определение «понижающий» в случае с ( i > 1 {\displaystyle i>1} ) и «повышающий» с ( i < 1 {\displaystyle i<1} ).

См. также

Литература

  1. Под ред. Скороходова Е. А. Общетехнический справочник. — М.: Машиностроение, 1982. — С. 416.
  2. Гулиа Н. В., Клоков В. Г., Юрков С. А. Детали машин. — М.: Издательский центр «Академия», 2004. — С. 416. — ISBN 5-7695-1384-5.
  3. Анурьев В. И. Справочник конструктора-машиностроителя: В 3 т. / Под ред. И. Н. Жестковой. — 8-е изд., перераб. и доп.. — М.: Машиностроение, 2001. — ISBN 5-217-02962-5.
  4. Курмаз Л. В. Детали машин. Проектирование// Л. В. Курмаз; А. Т. Скойбеда — 2-е изд., испр. и доп. — Мн.: УП «Технопринт», — 2002. — 296с.,ил.
  5. Чернавский С. А., Боков К. Н. Курсовое проектирование деталей машин. — 1988.

Передаточное отношение — это… Что такое Передаточное отношение?

Передаточное отношение() — одна из важных характеристик механической передачи вращательного движения, находится как отношение угловой скорости ведущего элемента () механической передачи к угловой скорости ведомого элемента() или отношение частоты вращения ведущего элемента () механической передачи к частоте вращения ведомого элемента () или отношение числа зубьев () (длины окружности, радиуса, диаметра) ведомого элемента к числу зубьев () (длине окружности, радиусу, диаметру) ведущего элемента механической передачи.

Характеристика передаточное отношение применима как к механической передаче с одной ступенью (одной кинематической парой), так и к механическим передачам со множеством ступеней. Во втором случае передаточное отношение всей механической передачи будет равно произведению передаточных отношений всех ступеней.[1]

Механизмы с передаточным отношением больше единицы — редукторы (понижающие редукторы), меньше единицы — мультипликаторы (повышающие редукторы).

Величина, обратная передаточному отношению, называется передаточное число().

Тем не менее, в нынешнее время понятия передаточное отношение и передаточное число означают одно и то же. Например, ГОСТы 16532-70, 21354-87 и др. величину () называют передаточным числом, а многие каталоги редукторов ту же величину называют передаточным отношением.

См. также

Литература

  1. Под ред. Скороходова Е. А. Общетехнический справочник. — М.: Машиностроение, 1982. — С. 416.
  2. Гулиа Н. В., Клоков В. Г., Юрков С. А. Детали машин. — М.: Издательский центр «Академия», 2004. — С. 416. — ISBN 5-7695-1384-5
  3. Анурьев В. И. Справочник конструктора-машиностроителя: В 3 т. / Под ред. И. Н. Жестковой. — 8-е изд., перераб. и доп.. — М.: Машиностроение, 2001. — ISBN 5-217-02962-5

Примечания

  1. ↑ Это неприменимо для планетарных передач.

ПЕРЕДАТОЧНОЕ ОТНОШЕНИЕ И ПЕРЕДАТОЧНОЕ ЧИСЛО

⇐ ПредыдущаяСтр 4 из 5Следующая ⇒

Важнейшей характеристикой всякого зубчатого механизма является передаточное отношение. Передаточным отношением называется отношение угловых скоростей колес. Передаточное отношение принято обозначать буквой U и снабжать индексами, указывающими номера зубчатых колес, например U12 = ω1 ⁄ ω2. Из рассмотрения зубчатой передачи на рис.5.23 следует:

VA1 = ω1 r1 VA2 = ω2 r2 VA1 = V A2

Тогда

U12 = ω1 / ω2 = r2 / r1 = m z2 / m z1 = z2 / z1 (5.10)

Передаточному отношению присваивается знак +, если входное и выходное колеса вращаются в одном направлении, и знак -, если они вращаются в разном направлении. Для зубчатой передачи внешнего зацепления U12 отрицательно, для внутреннего зацепления – положительно. При передаточном отношении больше единицы имеем редуктор (замедление скорости), при передаточном отношении меньше единицы – мультипликатор (происходит увеличение скорости вращения). В подавляющем большинстве случаев механизмы являются редукторами. Их назначение – уменьшать частоту вращения двигателя до той, которая необходима для нормальной работы исполнительного органа машины. Одновременно с уменьшением частоты вращения повышается крутящий момент. Так как к.п.д. зубчатой передачи очень высок (0.95 – 0.98), то можно считать, что мощности N1 = N2, где N1 = M1 ω1, N2 = M2 ω2, отсюда следует, что M2 = M1 U12.

Передаточное отношение не следует путать с передаточным числом, под которым понимается отношение угловой скорости большего колеса к угловой скорости меньшего, называемого обычно шестерней. Передаточное число всегда больше единицы и знака не имеет.

Рядовой зубчатой передачей (зубчатым рядом) называется зубчатый механизм, образованный зубчатыми колесами с неподвижными осями. Зубчатый ряд состоит из одной или нескольких зубчатых передач. Рассмотрим механизм на рис. 5.24. Он составлен из трех зубчатых передач, образованных колесами z1, z2, z3, z4, z5, z6. Запишем их передаточные отношения:

U12 = ω1./ ω2, U34 = ω3 / ω4, U45 = ω4 / ω5,

откуда

Ω2 = ω1 / U12, ω4 = ω3 / U34, ω5 = ω4 / U45

Производя последовательную подстановку выражений для ω2, ω4, ω5, получим

Ω5 = ω1 / U45 U34 U12,

откуда

U15 = U12 U34 U45

Полученная формула является частным случаем общего правила, формулируемого следующим образом:

Передаточное отношение рядовой зубчатой передачи равно произведению передаточных отношений входящих в нее зубчатых передач, при этом следует учитывать знаки передаточных отношений составляющих зубчатых передач.

Передаточное отношение также можно выразить через числа зубьев:

U15 = Z2 Z4Z5 / Z1 Z2 Z4 (5.11)

Отсюда следует второе правило:

Передаточное отношение рядовой зубчатой передачи равно дроби, в числителе которой стоят числа зубьев выходных колес, а в знаменателе – входных. Знак берется согласно указанному выше правилу знаков. В формуле колесо Z4 не влияет на численное значение передаточного отношения, но влияет на знак. Такое колесо называется паразитным

РАСЧЕТ РЯДОВОЙ КОРОБКИ ПЕРЕДАЧ

 
 

В качестве примера рассмотрим коробку передач легкового автомобиля, в основе которой рядовой зубчатый механизм (рис. 5.24).

Она состоит из входного вала 1, выходного вала 2 и промежуточного вала 3. На промежуточном валу жестко закреплены колеса с числом зубьев Z1 = 29, Z2 = 24, Z3 = 20, Z4 = 15, Z5 = 15, на входном валу – колесо Z6 = 17. На выходном валу подвижно установлены колеса Z7 = 24, Z8 = 27, Z9 = 33. Для включения передачи 1 рычагом переключения передач передвигается кулачковая муфта М1 направо так, что она кулачками сцепляется с колесом Z9. Передвигая муфту влево, включаем передачу II, аналогично посредством муфты М2 происходит включение передач III IY. При указанных числах зубьев колес рассчитаем передаточные отношения на I II III IY передачах:

UI = 29 33 / 17 15 = 3.75

UII = 29 27 / 17 20 = 2.303

UIII = 29 21/ 17 24 = 1.49

UIY = 1

Вводя в зацепление с колесами Z5 и Z10 = 34 паразитное колесо Z11, получаем передачу заднего хода с передаточным отношением

Uзх = — 29 34 / 17 15 = — 3.88.

ПЛАНЕТАРНЫЕ ЗУБЧАТЫЕ МЕХАНИЗМЫ

Планетарным называется зубчатый механизм, содержащий колеса с подвижными осями. Планетарные зубчатые механизмы широко распространены в технике, особенно транспортной, так как, обладая большим передаточным отношением, имеют малые габариты и вес. Иногда эти механизмы называют эпициклическими, так как траектории точек колес с подвижными осями при внешнем зацеплении представляют эпициклоиды. Простейший планетарный механизм представлен на рис. 5.25. Колесо 2 с подвижной осью называется сателлитом, центральное колесо 1 – солнечным, звено, несущее ось сателлита, называется водилом, его принято обозначать буквой Н.

 
 

 
 

Если колесо 1 подвижно, степень подвижности механизма, рассчитанная по формуле Чебышева, равна 2, Если остановить колесо 1, получим механизм с W = 1 (рис. 5.25б) Механизмы, у которых W>1, называются дифференциальными (зубчатыми дифференциальными). Если у планетарного механизма остановить водило, оставив колеса свободными, получим рядовую передачу.

Схема планетарных механизмов могут быть очень разнообразными. Практическое применение нашло, в основном, только несколько схем. Наиболее распространенные схемы представлены на рис. 5.26.

Механизм по схеме а получил название механизма Джеймса, а механизм по схеме в – механизм Давида. Наибольшее распространение получила схема а. Она характеризуется высоким к.п.д., практический диапазон передаточных отношений U = 3 – 8. Механизмы по схемам в и г могут иметь очень большие передаточные отношения, но у них низкий к.п.д. По схеме е выполняются мотор – редукторы, представляющие в одном агрегате двигатель и редуктор. Особенно перспективна схема д, здесь всего два колеса, высокий к.п.д., большое передаточное отношение.

АНАЛИТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОГО ОТНОШЕНИЯ И УГЛОВЫХ СКОРОСТЕЙ ПЛАНЕТАРНЫХ МЕХАНИЗМОВ

Кинематический расчет планетарных механизмов значительно более сложен, чем рядовых механизмов. Он основан на методе обращения движения. Рассмотрим его на примере механизма на рис. 5.27. Считаем, что заданы числа зубьев колес Z1, Z2, Z3, Z4, угловая скорость входного колеса ω1. Требуется определить передаточное отношение U1н, угловую скорость выходного звена Н и угловую скорость колеса 2.

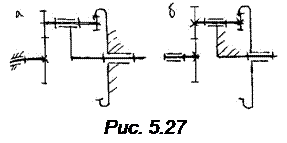Сущность метода обращения движения состоит в следующем: придадим стойке механизма скорость вращения водила ωн, но в противоположном направлении. Тогда водило окажется неподвижным в абсолютной системе отсчета, а остальные звенья приобретут дополнительную скорость – ωн. Изобразим обращенный механизм рядом на схеме. Механизм с неподвижным водилом является зубчатым рядом, для него справедливы полученные ранее соотношения:

U14H = (ω1 — ωH) / (ω4 – ωH) (5.12)

Здесь верхний индекс Н указывает, что параметры относятся к обращенному механизму. Согласно формуле (5.11) имеем:

U14H = — Z2 Z4 / Z1 Z3

Из формулы (5.12) после некоторых преобразований следует:

U1H = ω1 / ωH = 1 — U14H

Полученная формула справедлива для любой схемы планетарного механизма. Она носит название формулы Виллиса.

Если требуется определить передаточное отношение от водила к колесу 1, то, имея в виду, что UH1 = 1 / U1H, получим

Uh2 = 1 / (1 — U14H)

Зная U1H, можно найти ωН: ωН = ω1 / U1H. Для определения скорости ω2 следует рассмотреть одну ступень планетарного механизма и изобразить соответствующий ей обращенный механизм (рис.5.28). Для обращенного механизма

U12 = (ω1 – ωH) / (ω2 — ωH)

Отсюда уже не представляет сложности определить ω2.

5.25 КИНЕМАТИЧЕСКИЙ АНАЛИЗ АВТОМОБИЛЬНОГО ДИФФЕРЕНЦИАЛА

 
 

Рассмотренный метод кинематического исследования применим также к анализу дифференциальных зубчатых механизмов. Одним из наиболее известных является автомобильный дифференциал (рис.5.29). Его назначение – передача движения от карданного вала к колесам автомобиля. Механизм, представленный на рис.5.29, включает главную передачу, образованную коническими колесами Z1и Z2, корпус дифференциала, являющийся в то же время водилом дифференциального механизма, нескольких сателлитов Z4 и двух центральных колес Z3 и Z5, жестко посаженных на полуоси колес.

Применим к этому механизму принцип обращения движения, сообщив ему скорость – ωН. На рис. представлен обращенный механизм. Для него можно записать

U35H = (ω3 – ωH) / (ω5 – ωH) = Z5 / Z3

Поскольку Z5 = Z3, U35H = -1. Знак минус указывает, что колеса Z3 и Z5 в обращенном механизме вращаются в противоположном направлении. Произведя подстановку, получим уравнение автомобильного дифференциала:

Ω3 + ω5 = 2 ωН (5.13)

Произведем анализ формулы (5.13). При движении по прямому участку дороги ω3 = ω5 = ωН, следовательно, дифференциал как бы жестко связывает полуоси, происходит кинематическая блокировка дифференциала. Совершенно по другому ведет себя дифференциал при движении по закруглению. Внешнее колесо движется с большой угловой скоростью, чем внутренне, но так, что их средняя скорость равна скорости водила. Если бы колеса были связаны жесткой осью, происходило бы пробуксовка одного или обоих колес, ухудшая эксплуатацию автомобиля. В том случае, когда одно колесо свободно пробуксовывает, второе колесе неподвижно. Скорость буксующего колеса равно 2ωН. В таких случаях применят механическую блокировку дифференциала.




Передаточное отношение, передаточное число — Студопедия

Передаточное отношение – это отношение мгновенных угловых или линейных скоростей ведущего и ведомого звеньев. u = ω1/ω2.

Передаточное число – это отношение чисел зубьев или диаметров (радиусов) ведомого и ведущего звеньев. i = z2/z1.

В производственном лексиконе эти два понятия зачастую путают, поскольку в численном выражении u = i. Определим uи i при последовательном и параллельном соединении зубчатых колес.

Последовательное соединение (рис.4.3).

u 1-4 = ω1/ω2* ω2/ω3* ω3/ω4 = ω1/ω4

i 1-4 = z2/z1* z3/z2* z4/z3 = z4/z1

Видим, что промежуточные шестерни z2 иz3не влияют на передаточное отношение и передаточное число. Эти шестерни называются паразитными. Они

Рис. 4.3устанавливаются в двух случаях:

1 – для изменения направления вращения; 2 – для получения большого межосевого расстояния при малых поперечных габаритах передачи.

Параллельное соединение (рис.4.4).

u 1-4 = ω1/ω2* ω3/ω4 = ω1/ω4,

ω2 = ω3 – это один вал.

i 1-4 = z2/z1* z4/z3

При параллельном соединении нет паразитных шестеренок. Больше того, у зубчатых колес 1-й ступени (z1и z2) модуль меньше чем модуль колес 2-й ступени (z3и z4), поскольку крутящий момент на входе 1-й ступени в i 1-2 = z2/z1раз меньше момента на входе 2-й ступени (при условии, что обе

Рис. 4.4ступени редукторные, то есть

z2 > z1 ; z4 > z3 , соответственно i 1-2 > 1и i 3-4 > 1).

Редуктор –понижает обороты, но увеличивает крутящий момент.

Мультипликатор – повышает обороты, но понижает крутящий момент.

Передаточное число — это… Что такое Передаточное число?

Передаточное число () является величиной, обратной передаточному отношению, и рассчитывается как отношение числа зубьев ведомой шестерни () к числу зубьев ведущей шестерни (), а также, как отношение длин окружностей в сечении (или радиусов окружностей в сечении) в точке зацепления, ведущего вала по отношению к ведомому в ремённой или фрикционной передаче. Вместо количества зубьев правильней использовать эффективные длины окружностей, или радиусы шестерней, которые определяют передачу вращающего движения, аналогично формуле для фрикционной передачи. По сути формула отношения числа зубьев является частным случаем отношения эффективных длин окружностей, вписанных в шестерни, находящиеся в зацеплении.

В современное время понятие передаточное число практически не применяется. Зачастую передаточное отношение называют передаточным числом. Например, в статье Планетарная передача применяются оба понятия, обозначая одно и то же.

См. также

Литература

  1. Под ред. Скороходова Е. А. Общетехнический справочник. — М.: Машиностроение, 1982. — С. 416.
  2. Гулиа Н. В., Клоков В. Г., Юрков С. А. Детали машин. — М.: Издательский центр «Академия», 2004. — С. 416. — ISBN 5-7695-1384-5
  3. Анурьев В. И. Справочник конструктора-машиностроителя: В 3 т. / Под ред. И. Н. Жестковой. — 8-е изд., перераб. и доп.. — М.: Машиностроение, 2001. — ISBN 5-217-02962-5

Примечания

Как работают передаточные числа?

Передаточное число — это фундаментальная наука, лежащая в основе почти каждой машины в современную эпоху. Они могут максимизировать мощность и эффективность и основаны на простой математике. Итак, как они работают?

Если вы работаете с передаточными числами каждый день, этот пост, вероятно, не для вас. Но если вы хотите улучшить свое понимание этого важного элемента конструкции машины, продолжайте читать.

Передаточные числа просты, если вы понимаете математику, стоящую за кругами.Я избавлю вас от математики в начальной школе, но важно знать, что длина окружности связана с диаметром круга. Эта математика важна при расчете передаточного числа.

Основы расчета передаточных чисел и передаточных чисел

Чтобы начать понимать передаточные числа, проще всего начать с удаления зубьев с шестерен. Представьте себе два круга, катящихся друг против друга, при условии отсутствия проскальзывания, как в колледже Физика 1. Дайте одному кругу диаметр 2,54 дюйма .Умножение этого числа на пи дает нам окружность 8 дюймов или, другими словами, один полный оборот окружности приведет к смещению 8 дюймов .

Обозначьте круг два диаметром ,3175 дюйма , что даст нам окружность 1 дюйм . Если эти два круга катятся вместе, они будут иметь передаточное число 8: 1, так как первый круг имеет окружность в 8 раз больше , чем второй круг. Передаточное число 8: 1 означает , что круг два вращается 8 раз по за каждый раз, когда круг один вращается.Не засыпай меня еще; мы будем становиться все более и более сложными.

Шестерни — это не круги, потому что, как вы знаете, у них есть зубцы. Шестерни должны иметь зубья, потому что в реальном мире не существует бесконечного трения между двумя вращающимися кругами. Зубья также позволяют легко достичь точного передаточного числа.

Вместо того, чтобы иметь дело с диаметром шестерен, вы можете использовать количество зубьев шестерни для достижения высокоточных передаточных чисел.Передаточные числа никогда не бывают произвольными, они сильно зависят от необходимого крутящего момента и выходной мощности, а также от зубчатой ​​передачи и прочности материала. Например, если вам нужно передаточное число 3,57: 1 , можно спроектировать две совместимые шестерни , одну с 75 зубьями, и другую с 21 .

СВЯЗАННЫЙ: ДАННЫЙ ТУРБОФАН С ПЕРЕДАЧЕЙ НА 15 ПРОЦЕНТОВ ЭФФЕКТИВнее ДРУГИХ ДВИГАТЕЛЕЙ САМОЛЕТОВ

Еще одним важным аспектом, влияющим на использование зубьев в зубчатых колесах, являются производственные допуски. Большинство шестерен могут изготавливаться с довольно широкими допусками, и мы знаем, что чем жестче допуск, тем дороже их производство. Зубья позволяют производить шестерни заданного диаметра в некотором роде, а это означает, что производство дешевле. По сути, зубья становятся буфером, который допускает дефекты в производстве зубчатых колес.

Расчет передаточных чисел при проектировании машин

Хотя базовое передаточное число довольно просто понять, оно также может быть намного сложнее.При проектировании машин часто требуются большие пролеты шестерен, называемые зубчатыми передачами. Они состоят из множества шестерен, которые часто ставятся друг на друга или кладутся последовательно. Зубчатые передачи необходимы для достижения более надежных передаточных чисел, а также для влияния на направление вращения. Поскольку две соединенные шестерни будут вращаться в противоположных направлениях, зубчатые передачи часто необходимы для передачи мощности через определенные передаточные числа без влияния на вращение.

Например, при использовании трехступенчатой ​​зубчатой ​​передачи , с передаточным числом 1: 5, приведет к увеличению скорости вращения 2500% при сохранении того же направления, что и вход.Чтобы дать более конкретный пример, двигатель, который прикладывал 100 об / мин к начальному концу этой зубчатой ​​передачи, будет выдавать 2500 об / мин на другом конце в том же направлении. Вы также можете изменить направление подачи питания и понизить двигатель 2500 об / мин до выходной мощности 100 об / мин . Эти изменения позволяют регулировать крутящий момент и скорость.

СВЯЗАННЫЕ С: ФУТУРИСТИЧЕСКОЕ РОССИЙСКОЕ ПЕХОТНОЕ ОБОРУДОВАНИЕ ПОЛУЧАЕТ ЯДЕРНУСТОЙЧИВОЕ ОБНОВЛЕНИЕ

Более сложные комбинации шестерен и передаточных чисел позволяют получить некоторые интересные конструкции машин.Теоретически передаточные числа просты, но, как инженер, вы можете оказаться вовлеченным в сложные конструкции зубчатых передач, которые кажутся немного подавляющими. Как и в случае с другими инженерными навыками, для полного развития навыков проектирования передаточных чисел требуется время.

Коробки передач — практическое применение передаточных чисел

Коробки передач — одни из лучших примеров практического применения передаточных чисел. Любой, кто ездил на машине или другом моторизованном транспортном средстве, получил пользу от трансмиссии в той или иной форме.И каждая трансмиссия — это, по сути, просто набор тесно связанных шестерен и передаточных чисел. Посмотрите невероятно полезное видео из Learn Engineering ниже, чтобы узнать больше о том, как работают механические коробки передач.

Важно отметить, что, хотя механические коробки передач перестают пользоваться популярностью у автопроизводителей, поскольку их нелегко установить в гибридные или электромобили, они работают почти так же, как автоматические трансмиссии, в том, что касается передачи. ,Основное отличие состоит в том, как переключаются передачи.

СВЯЗАННЫЕ: ПЯТЬ ТЕНДЕНЦИЙ, ФОРМИРУЮЩИХ АВТОМОБИЛЬНУЮ ПРОМЫШЛЕННОСТЬ В 2020 ГОДУ

Механические трансмиссии будут включать в себя действия пользователя (перемещение рычага переключения передач и сцепления) для переключения, тогда как автоматические трансмиссии будут использовать ввод от бортового компьютера автомобиля или, в очень редких случаях. ранние модели, механическое воздействие либо от скорости автомобиля, либо от двигателя автомобиля.

.

Передаточное отношение — AccountingTools

Передаточное отношение измеряет соотношение заемных средств компании к ее собственному капиталу. Коэффициент указывает на финансовый риск, которому подвергается бизнес, поскольку чрезмерная задолженность может привести к финансовым трудностям. Высокое соотношение заемных средств представляет собой высокую долю заемных средств к собственному капиталу, в то время как низкое соотношение заемных средств представляет собой низкую долю заемных средств к собственному капиталу. Это соотношение аналогично соотношению заемных и собственных средств, за исключением того, что существует ряд вариаций формулы коэффициента заемного капитала, которые могут дать несколько иные результаты.

Высокий коэффициент заемного капитала свидетельствует о большом левередже, когда компания использует заемные средства для оплаты своих продолжающихся операций. В условиях экономического спада у таких компаний могут возникнуть проблемы с соблюдением графиков погашения долга, и они могут рисковать банкротством. Ситуация особенно опасна, когда компания участвует в долговых соглашениях с плавающими процентными ставками, когда внезапное повышение ставок может вызвать серьезные проблемы с выплатой процентов.

Высокий коэффициент заемных средств не вызывает особого беспокойства в регулируемой отрасли, такой как коммунальное предприятие, где бизнес находится в монопольной ситуации, и его регулирующие органы, вероятно, одобрят повышение ставок, которое гарантирует его дальнейшее выживание.

Кредиторы особенно обеспокоены передаточным отношением заемных средств, поскольку чрезмерно высокий коэффициент заемного капитала подвергает их кредиты риску невозврата. Возможные требования со стороны кредиторов для противодействия этой проблеме включают использование ограничительных условий, запрещающих выплату дивидендов, принуждение избыточного денежного потока к погашению долга, ограничения на альтернативное использование денежных средств и требование к инвесторам вкладывать больше капитала в компанию. Кредиторы испытывают аналогичное беспокойство, но обычно не могут изменить поведение компании.

Отрасли с большими постоянными потребностями в основных средствах обычно имеют высокие коэффициенты заемного капитала.

Низкий коэффициент заемных средств может указывать на консервативное управление финансами, но также может означать, что компания находится в высокоцикличной отрасли и поэтому не может позволить себе чрезмерно расширяться перед лицом неизбежного спада продаж и прибыли.

Как рассчитать коэффициент заемного капитала

Наиболее полная форма коэффициента заемного капитала — это та, где все формы долга — долгосрочные, краткосрочные и даже овердрафты — делятся на собственный капитал.Расчет выглядит следующим образом:

(Долгосрочная задолженность + Краткосрочная задолженность + Банковские овердрафты) ÷ Акционерный капитал

Другая форма коэффициента заемного капитала — это коэффициент, умноженный на процентный доход, который рассчитывается, как показано ниже, и предназначен для обеспечения некоторое указание на то, может ли компания генерировать достаточно прибыли для оплаты текущих процентных платежей.

Прибыль до уплаты процентов и налогов ÷ Проценты к уплате

Еще одним изменением коэффициента заемного капитала является отношение долгосрочного долга к собственному капиталу; это не особенно полезно, когда у компании есть большой краткосрочный долг (что особенно характерно, когда ни один кредитор не желает брать на себя обязательства по долгосрочному кредитованию).Однако это может быть полезно, когда большая часть долга компании связана с долгосрочными облигациями.

Пример заемного капитала

В первый год ABC International имеет 5 000 000 долларов долга и 2 500 000 долларов акционерного капитала, что является очень высоким 200% -ным коэффициентом заемного капитала. В течение 2-го года ABC продает больше акций в рамках публичного предложения, в результате чего база собственного капитала намного превышает 10 000 000 долларов. Уровень долга остается неизменным во 2-м году. Это означает, что коэффициент заемного капитала составляет 50% во 2-м году.

Как уменьшить заемные средства

Существует ряд методов, доступных для уменьшения передаточного отношения компании, в том числе:

  • Продать акции .Совет директоров может разрешить продажу акций компании, которые могут быть использованы для выплаты долга.

  • Конвертировать ссуды . Проведите переговоры с кредиторами об обмене существующей задолженности на акции компании.

  • Уменьшить оборотный капитал . Увеличьте скорость сбора дебиторской задолженности, сократите уровни запасов и / или увеличьте количество дней, необходимых для оплаты кредиторской задолженности, в любом из которых появляются денежные средства, которые можно использовать для погашения долга.

  • Увеличить прибыль . Используйте любые доступные методы для увеличения прибыли, которые должны генерировать больше денег для погашения долга.

Похожие термины

Заработок также известен как кредитное плечо.

Связанные курсы

Справочник по бизнес-показателям
Интерпретация финансовой отчетности

.

Как рассчитать передаточное число

  • Дом
  • Категории
    • Принадлежности
      • Аксессуары для интерьера
      • Внешние аксессуары
      • Игрушки
    • Очистка и детализация
    • Электроника
      • Аудио
    • Двигатель и производительность
    • Инструменты
    • Шины и диски
    • Мотоциклы и велосипеды
    • Уход на дому
    • Кемперы на колесах
    • Внедорожники
    • Гарантии
      • Расширенные гарантии
      • Заводские гарантии
  • Блог
  • Инструменты
    • Калькулятор размера шин
    • Поиск колес и шин
  • О нас
  • Связаться